1 Введение
В данном курсе изучается физика строения вещества на микроуровне. В значительной части затрагиваемые в нём темы пересекаются с курсом квантовой механики. Отличие заключается, во-первых, в порядке изложения, а во-вторых, в его стиле. В курсе атомной физики мы будем придерживаться в основном исторической логики изложения, местами, возможно, в ущерб лучшей методологичности. Кроме того, изложение будет идти на более качественном уровне с минимальным привлечением математического аппарата.
Впервые проблема строения вещества на микроуровне была поднята ещё древнеиндийскими и древнегреческими философами. В Древней Греции Левкипп и его ученик Демокрит Абдерский ввели понятие атомизма. Согласно их учению, существуют только атомы и пустота. Атомы — мельчайшие неделимые частицы. Сторонниками атомизма были также Платон и Эпикур. Противники атомизма Демокрита утверждали, что материя делится до бесконечности. Аристотель, Анаксагор, а позднее также Декарт и Лейбниц, придерживались мнения, что вещество бесконечно делимо.
В XVII и XVIII веках химикам удалось экспериментально подтвердить идею атомизма, показав, что некоторые вещества не могут быть подвергнуты дальнейшему расщеплению на составляющие элементы с помощью химических методов. В 1661 году Роберт Бойль создал труд «Химик-скептик», в котором объяснил разность свойств различных веществ тем, что они построены из разных частиц (корпускул). В 1811 году Авогадро выдвинул гипотезу о том, что молекулы элементарных газов состоят из двух одинаковых атомов; позднее на основе этой гипотезы Канниццаро осуществил реформу атомно-молекулярной теории, которая была утверждена на первом международном съезде химиков в 1860 году. В 1869 году Д. И. Менделеев открыл периодический закон химических элементов, он же показал зависимость свойств химических элементов от их атомной массы.
Конец XIX века: целый ряд экспериментов, указывающих на атомарность и квантовость микромира
Начало XX века: начало формирования современной физики микромира, становление квантовой механики
1.1 Важные открытия
1874 — Джордж Джонстон Стони из чисел Фарадея и Авогадро определил величину элементарного заряда и в 1891 году ввёл термин «электрон».
1888 — Столетов исследует явление фотоэффекта.
1895 — Вильгельм Рентген открывает рентгеновские лучи.
1896/7 — Джозеф Джон Томсон и независимо от него Эмиль Вихерт экспериментально доказали существование электрона, измерив отношение его заряда к массе.
1900 — Макс Планк создаёт квантовую теорию излучения абсолютно чёрного тела и вводит константу h.
1905 — Альберт Эйнштейн объясняет фотоэлектрический эффект, постулируя существование «квантов» света.
1906–1911 — Эрнест Резерфорд измеряет размеры атомного ядра и выдвигает планетарную теорию строения атома.
1913 — Нильс Бор уточняет модель атома Резерфора, выдвигая ряд гипотез, в том числе квантованность состояния электрона в атоме.
1925–1927 — закладываются основы современной квантовой теории (Гейзенберг, Борн, Дирак, Паули, Шрёдингер).
1.2 Проблемы классической механики
Можно выделить три основных задачи, решение которых потребовало отказаться от классических представления о строении вещества:
- тепловое излучение нагретых тел
- фотоэлектрический эффект
- стабильность и свойства атома
2 Проблема теплового излучения
Тепловое излучение — это электромагнитное излучение, возникающее за счёт внутренней энергии тела. Любое нагретое тело излучает — это излучение и носит название теплового. Если тело находится в термодинамическом равновесии со своим излучением, то есть излучает столько же энергии в единицу времени, сколько получает в результате его поглощения, то такое тепловое излучение называется равновесным.
Проблема теоретического описания теплового излучения становится особенно острой с развитием массового производства электрических и газовых ламп в конце XIX века, требовавшего создания стандартов интенсивности освещения.
2.1 Характеристики электромагнитного излучения
Для дальнейших выкладок необходимо ввести несколько характеристик теплового излучения.
Во-первых, введём плотность энергии электромагнитного излучения: \[ u = \frac{dE}{dV} \]
Её можно разложить в спектр по частотам излучения: \[ u = \int u_\nu d\nu \] величина \(u_\nu\) носит название спектральной плотности электромагнитной энергии.
Ещё одной важной величиной является интенсивность излучения или плотность потока электромагнитной энергии — это количество энергии, переносимой излучением в единицу времени через единичную площадку, перпендикулярную направлению распространения: \[ I = \frac{dE}{dtdS} \] В рамках электродинамики показывается, что выполняется следующее соотношение: \[ I = \frac{c}{4\pi}u, \] где \(c\) — скорость света.
Для характеристики излучающей поверхности тела вводят величину энергетической светимости \(S\), равную средней мощности излучения, испускаемой единицей площади поверхности. Можно показать, что имеется следующая связь между энергетической светимостью поверхности и интенсивностью излучения вблизи неё: \[ S = \pi I = \frac{cu}{4} \]
2.2 Свойства равновесного излучения
Экспериментально было обнаружено, что тепловое излучение, находящееся в термодинамическом равновесии с внутренними стенками полости, внутри которой это излучение заперто, обладает следующими свойствами:
- \(u\) и \(u_\nu\) не зависят от материала и свойств стенок полости, а зависят только от температуры её внутренних стенок;
- излучение однородно, изотропно, неполяризовано.
Таким образом, можно говорить о температуре излучения как о его универсальной характеристике равной температуре стенок полости.
2.3 Закон излучения Кирхгофа
Установлен Густавом Кирхгофом в 1859 году.

В современной формулировке закон звучит следующим образом:
Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы.
Или в математической форме: \[ \frac{s(\nu,T)}{a(\nu,T)} = f(\nu,T) \] где \(a(\nu,T)\) — поглощательная способность тела (доля падающей энергии, поглощаемой телом), \(s(\nu,T)\) — излучательная способность тела (энергия, излучаемая единицей площади в единицу времени), \(f(\nu,T)\) — универсальная функция, не зависящая от тела.
Этот закон несложно получить из простых соображений. Рассмотрим полость, стенки которой имеют некую фиксированную температуру. Они излучают электромагнитные волны и их же поглощают. Пусть \(K\) — количество электромагнитной энергии, воздействующей на единицу поверхности стенок в единицу времени. Из всей этой энергии некая часть \(A\) будет поглощена. Если обозначить через \(S\) энергию, излучаемую той же поверхностью в единицу времени, то в состоянии равновесия должно выполняться: \[ AK = S \] Чтобы перейти к спектральным плотностям, разложим эти величины в ряд по частоте: \(K = \int f(\nu, T)d\nu\), \(A = \int a(\nu, T)d\nu\), \(S = \int s(\nu, T)d\nu\) и применим принцип детального равновесия: если выполняется равенство для интегральной величины, то должно выполняться равенство и для каждой частоты или длины волны. Отсюда мы и получим математическое выражение закона Кирхгофа.
2.4 Абсолютно чёрное тело
В связи с законом Кирхгофа важной оказывается абстракция, известная как абсолютно чёрное тело — это физическое тело, которое при любой температуре поглощает всё падающее на него электромагнитное излучение во всех диапазонах.
Действительно, поскольку абсолютно чёрное тело поглощает всё падающее на него излучение, то для него \(a(\nu,T) \equiv 1\), то есть функция \(f(\nu,T)\) совпадает с излучательной способностью абсолютно чёрного тела, что делает задачу её поиска фундаментально важной.
Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Термин введён Густавом Кирхгофом в 1862 году.
Абсолютно чёрное тело — это модель, в реальности таких тел не сушествует. Наиболее близкого соответствия можно добиться при помощи непрозрачной замкнутой полости с небольшим отверстием, стенки которой имеют одинаковую температуру.
2.5 Законы равновесного излучения абсолютно чёрного тела
2.5.1 Закон Стефана — Больцмана
Закон открыт сначала эмпирически Йозефом Стефаном в 1879 году, и через пять лет выведен теоретически Людвигом Больцманом на основе второго принципа термодинамики в предположении пропорциональности плотности энергии излучения его давлению \(p = \frac{1}{3}u\).
Закон связывает плотность равновесного теплового излучения абсолютно чёрного тела с его температурой: \[ u = a T^4 \] где \(a\) — постоянная плотности излучения. Чаще, однако, эта формула применяется в другом виде, а именно, для мощности излучения единицы площади поверхности абсолютно чёрного тела: \[ S = \frac{cu}{4} = \sigma T^4 \] где \(\sigma = ca/4 = 5.670367(13)\times 10^{-8}~\frac{\text{Дж}}{\text{с}\cdot\text{м}^2\cdot\text{К}^4}\) — постоянная Стефана — Больцмана.
2.5.2 Первый закон Вина
Или общая формула Вина. Закон выведен Вильгельмом Вином в 1893 году из достаточно общих термодинамических соображений и электромагнитной теории света.

Согласно этому закону, спектральная плотность излучения абсолютно чёрного тела выражается следующей формулой: \[ u_\nu = \nu^3 \Phi\left(\frac{\nu}{T}\right), \] где \(\Phi(x)\) — неизвестная на тот момент функция.
Из этой формулы можно вывести закон Стефана — Больцмана: \[ u = \int u_\nu d\nu = \int \nu^3 \Phi\left(\frac{\nu}{T}\right) d\nu = T^4 \int \xi \Phi(\xi) d\xi = \sigma T^4 \]
2.5.3 Закон смещения Вина
На основе первого закона Вина можно вывести зависимость частоты (и длины волны), на которой наблюдается максимум излучения, от температуры тела: \[ \frac{du_\nu}{d\nu} = \frac{d}{d\nu}(\nu^3\Phi) = 0 \] \[ 3\nu^2\Phi + \nu^3\frac{1}{T}\Phi^\prime = 0 \] \[ 3\Phi +\frac{\nu}{T}\Phi^\prime = 0 \] Решением данного уравнения является некая величина \(\nu_{max}\), которая пропорциональна температуре. Аналогичный вывод можно провести и для разложения плотности излучения по длинам волнам и получить: \[\lambda_{max} = \frac{b}{T}\] Этот закон и носит название закона смещения Вина. Коэффициент \(b\) называется постоянной Вина и равен \(0,002898~\text{м}\cdot\text{К}\).
2.5.4 Второй закон Вина
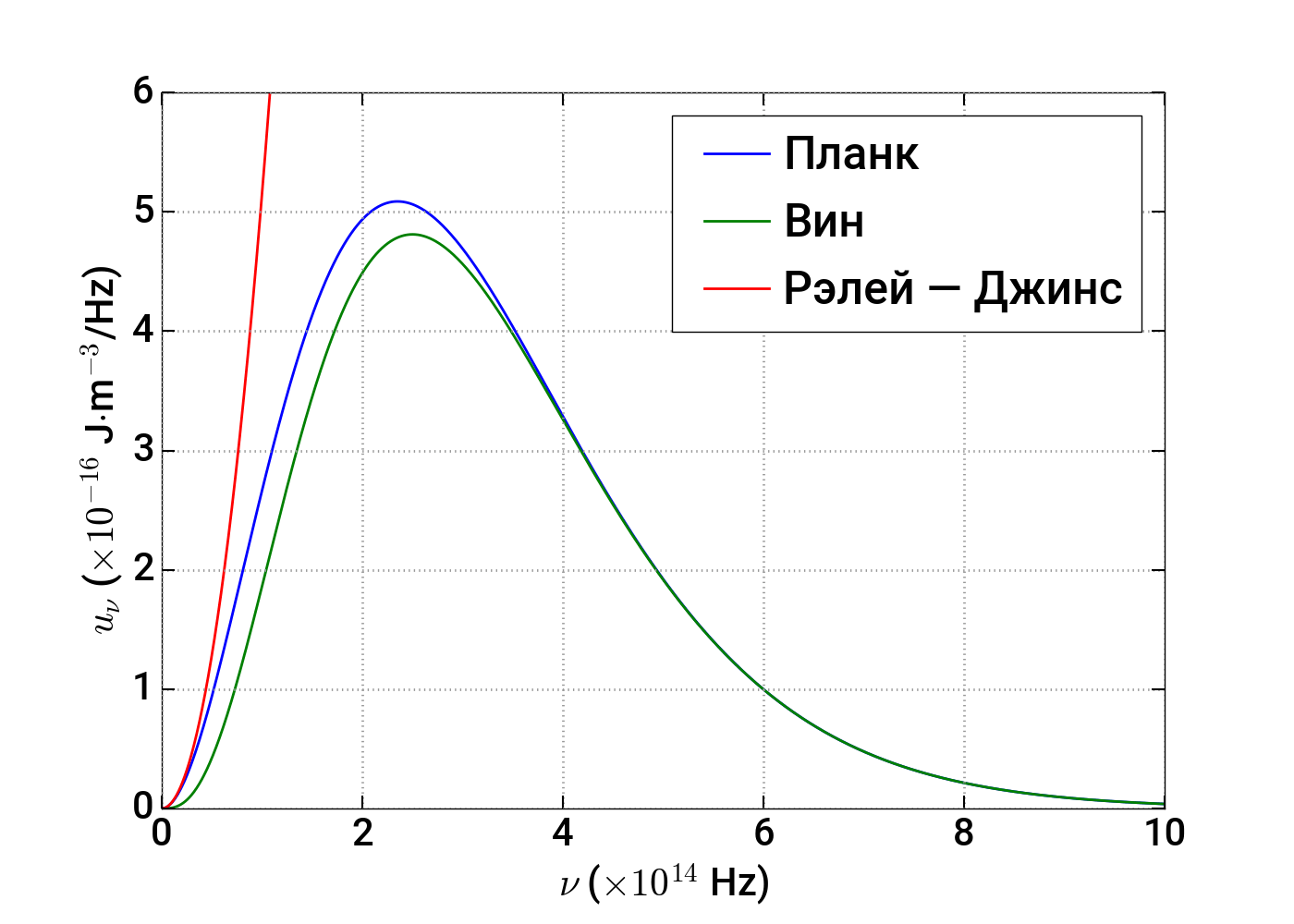
Или частная формула Вина. В 1896 году Вин на основе дополнительных предположений вывел свой второй закон излучения: \[ u_\nu = C_1 \nu^3 e^{-C_2\frac{\nu}{T}} \] где \(C_1\), \(C_2\) — некий универсальные константы. Видно, что он удовлетворяет первому закону Вина, однако сравнение с опытом показало, что эта формула справедлива лишь в пределе достаточно высоких частот (малых длин волн). Первыми это продемонстрировали Отто Люммер и Фердинанд Курльбаум в 1898 году.

2.5.5 Закон Рэлея — Джинса
В 1900 году лорд Рэлей предпринял попытку вывести закон излучения абсолютно чёрного тела из классических представлений об электромагнитном излучении. Повторим его рассуждения с учётом также дополнений, сделанных в 1905 году Джеймсом Джинсом.
Рассмотрим полость объёмом \(V\), не содержащую вещества и имеющую зеркальные стенки (для установления термодинамического равновесия необходимо поглощение, но его можно добавить не слишком сильно возмутив систему, например, помещением малой пылинки в полость). Излучение в полости можно представить в виде системы стоячих волн всевозможных частот (их называют модами). Рассчитаем количество таких волн, имеющих некую частоту \(\nu\).
В одномерном случае в ящике длиной \(l_x\) могут существовать только такие волны, для которых выполняется: \[l_x = n_x \frac{\lambda}{2}\] \[k_x = \frac{2\pi}{\lambda} = n_x \frac{\pi}{l_x}\] Если мы добавим второе измерение и рассмотрим прямоугольную полость, то волновой вектор можно разбить на две компоненты, для которых будет выполняться: \[k_x = n_x \frac{\pi}{l_x}\] \[k_y = n_y \frac{\pi}{l_y}\] В трёхмерном случае добавится ещё: \[k_z = n_z \frac{\pi}{l_z}\] При этом полная длина волнового вектора равна \[k^2 = k_x^2 + k_y^2 + k_z^2\] При изменение индексов \(n_x\), \(n_y\), \(n_z\) на единицу, мы смещаемся в \(k\)-пространстве соответственно на \(\frac{\pi}{l_x}\), \(\frac{\pi}{l_y}\), \(\frac{\pi}{l_z}\), таким образом, на каждую моду в этом пространстве приходится объём равный \(\frac{\pi}{l_x}\cdot\frac{\pi}{l_y}\cdot\frac{\pi}{l_z} = \frac{\pi^3}{l_xl_yl_z} = \frac{\pi^3}{V}\). Этот вывод сохраняется и для полостей произвольной формы.
Волны, частота которых лежит в интервале \([\nu, \nu+d\nu]\), образуют в \(k\)-пространстве сферический слой радиусом \(k=\frac{2\pi\nu}{c}\) и толщиной \(dk=\frac{2\pi d\nu}{c}\). Его объём: \(4\pi k^2dk\), соответственно, число мод, попадающих в этот объём (и имеющих частоту \(\nu\)): \[dN = 2\cdot\frac{1}{8}\cdot\frac{4\pi k^2dk}{\pi^3/V}\] где множитель \(2\) отвечает двум возможным поляризациям, а \(\frac{1}{8}\) учитывает, что волны, в которых одна или несколько проекций волнового вектора отличаются только знаком — это одна и та же мода. Окончательно получаем: \[dN_\nu = \frac{8\pi V \nu^2d\nu}{c^3}\]
Ключевой идеей вывода является предположение о том, что энергия излучения должна подчиняться теореме о равнораспределении энергии по степеням свободы. то есть на каждую моду должна приходиться одна и та же энергия равная \(2\cdot\frac{kT}{2}\), где \(2\) отвечает наличию в электромагнитной волне электрического и магнитного полей (или представлению о стоячей волне как об осцилляторе). Таким образом, на частоту излучения \(\nu\) приходится энергия равная: \[dE_\nu = kT\cdot dN_\nu = \frac{8\pi V kT \nu^2d\nu}{c^3}\] По определению спектральной плотности энергии имеем: \[u_\nu = \frac{dE_\nu}{Vd\nu} = \frac{8\pi}{c^3}\nu^2kT\] Этот закон и носит название закона Рэлея — Джинса. Несложно показать, что он удовлетворяет первому закону Вина для функции \(\Phi\) вида: \[\Phi\left(\frac{\nu}{T}\right) = \frac{8\pi}{c^3}\frac{kT}{\nu}\] Летом 1900 года Фердинанд Курльбаум и Генрих Рубенс провели измерения, которые показали, что в длинноволновой (инфракрасной) области излучение подчиняется закону Рэлея — Джинса, но не подчиняется второму закону Вина.

Фундаментальная проблема с законом Рэлея — Джинса была впервые акцентирована, однако, только в 1906 году Паулем Эренфестом, который вывел его независимо. Если проинтегрировать плотность излучения по всем частотам, то получится бесконечность. Это означает, что тело никогда не придёт в тепловое равновесие со своим излучением. Этот вывод, однако, противоречит экспериментальным данным. Поэтому проблему классического описания излучения Эренфест назвал «ультрафиолетовой катастрофой». Связана она с тем, что в классической физике число степеней свободы электромагнитного излучения бесконечно, а число степеней свободы тела — конечно, поэтому рано или поздно вся энергия должна сконцентрироваться в излучении.

2.5.6 Закон излучения Планка
7 октября 1900 года Рубенс рассказал о своих последних экспериментах и возникших проблемах Максу Планку.

Уже на следующий день Планк отправил в ответ открытку с новой формулой: \[ u_\nu = C \frac{\nu^3}{e^{\alpha\nu/T}-1} \] Через несколько дней Рубенс сообщил Планку, что формула с высокой точностью совпадает с экспериментальными данными. В течение нескольких следующих недель Планк активно искал способ обосновать эту формулу теоретически. Результаты своего исследования он представил уже 14 декабря 1900 года на заседании Немецкого физического общества. Именно этот день сейчас принято считать «днём рождения» квантовой теории.
Планк понимал, что необходимо каким-то образом побороть проблему бесконечного числа степеней свободы у излучения. Это можно было сделать разными способами, но не все приводили к нужной формуле. В конце концов Планку удалось обнаружить относительно простой способ обойти проблему. Для этого ему пришлось ввести гипотезу квантования энергии излучения.
Гипотеза заключалась в том, что излучение (и поглощение) света происходит не непрерывно, а конечными порциями, которые получили название «квантов» света или энергии. Если представить каждую моду электромагнитного излучения в полости как гармонический осциллятор, то его энергия тогда может принимать только дискретный набор значений (спектр) энергии — \(E_n = 0, E_0, 2E_0,\dots, nE_0,\dots\) где \(E_0\) — «квант» энергии, который может зависеть только от частоты соответствующего осциллятора.
Гипотеза Планка приводит к изменению величины энергии, приходящейся на одну моду. Если в классической физике она всегда равнялась \(kT\), то теперь она зависит от того, с какой вероятностью энергия моды равна каждому из значений спектра энергии этой моды. Из самых общих соображений эта вероятность должна подчиняться распределению Больцмана: \[ P(E_n) = A \exp\left(-\frac{E_n}{kT}\right) \] Константу \(A\) можно найти из очевидного условия: \[ \sum\limits_{n=0}^{\infty}P(E_n) = 1 \] \[ A = \frac{1}{\sum\limits_{n=0}^{\infty} \exp\left(-\frac{E_n}{kT}\right)} \] Тогда для средней энергии осциллятора получаем: \[ \left\langle E\right\rangle = \sum\limits_{n=0}^{\infty}E_nP(E_n) = \frac{\sum\limits_{n=0}^{\infty}nE_0\exp\left(-\frac{E_n}{kT}\right)}{\sum\limits_{n=0}^{\infty}\exp\left(-\frac{E_n}{kT}\right)} = \left[\beta=\frac{1}{kT}\right] = \] \[ =-\frac{d}{d\beta}\ln\sum\limits_{n=0}^{\infty}\exp\left(-\beta{E_n}\right)= -\frac{d}{d\beta}\ln\frac{1}{1-e^{-\beta E_0}}= E_0\frac{e^{-\beta E_0}}{1-e^{-\beta E_0}} \] Окончательно получаем: \[ \left\langle E\right\rangle = \frac{E_0}{e^{\beta E_0}-1} \] Это выражение необходимо использовать в выводе Рэлея — Джинса вместо \(kT\), следовательно, получаем следующую формулу: \[u_\nu = \frac{8\pi\nu^2}{c^3} \frac{E_0}{e^{\beta E_0}-1}\] Чтобы она удовлетворяла первому закону Вина, необходимо предположить, что \(E_0\sim\nu\). Обозначив коэффициент пропорциональности буквой \(h\), получаем окончательно формулу, известную теперь как формула Планка: \[u_\nu = \frac{8\pi h\nu^3}{c^3} \frac{1}{e^{h\nu/kT}-1}\] Константа \(h\) получила название постоянной Планка. Её можно получить из экспериментальных данных, если вывести из формулы Планка закон смещения Вина и закон Стефана — Больцмана и сравнить значения входящих в них констант с экспериментальными данными. По современным представлениям постоянная Планка имеет следующее значение: \[h = 6,626070040(81)\times 10^{-34}~\text{Дж}\cdot\text{с}\]
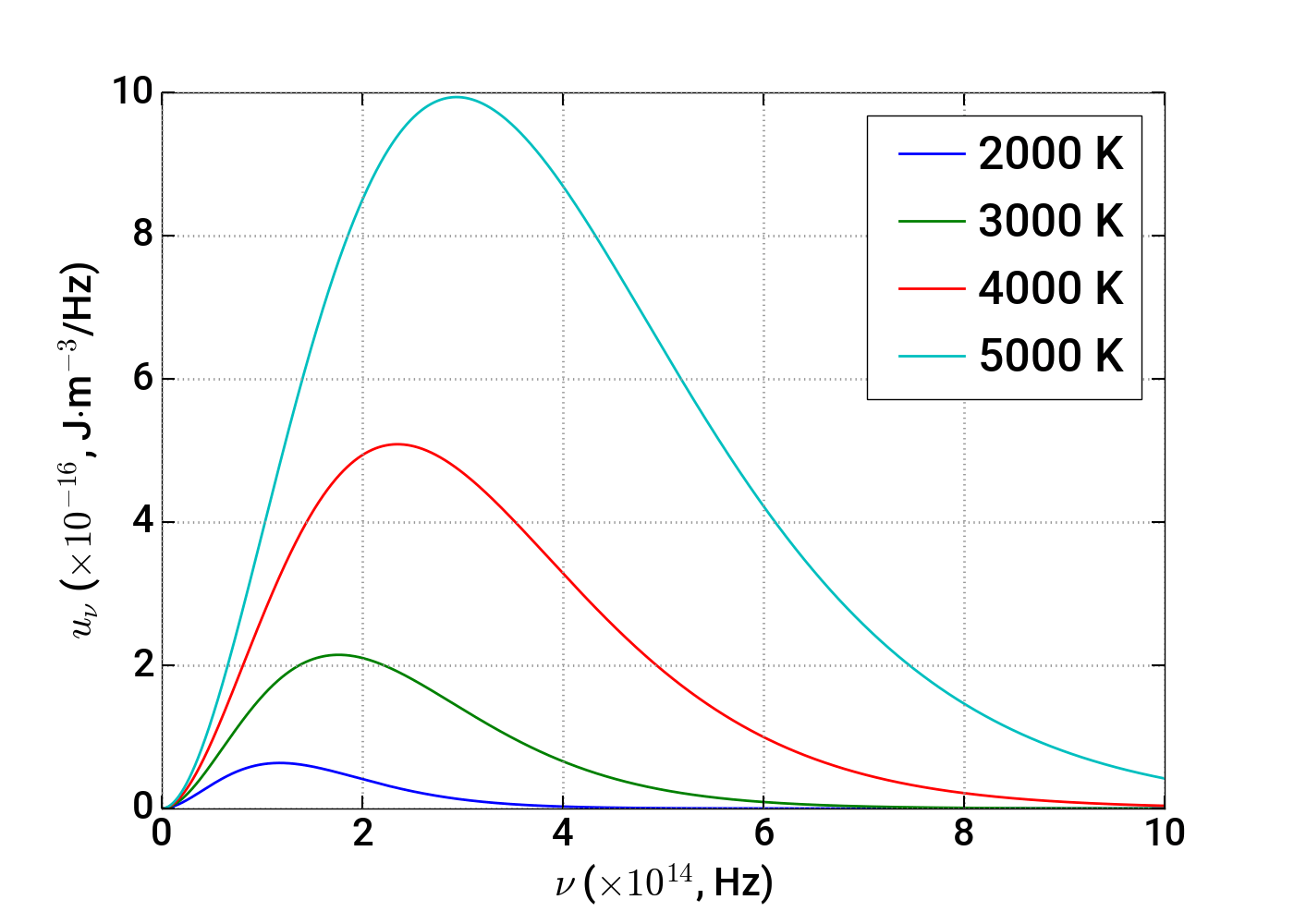
Часто, особенно в теоретических выкладках, используют разложение излучения в спектр по круговым частотам \(\omega = 2\pi\nu\). Получить это распределение (мы его обозначим \(u_\omega\)) из формулы выше можно, если учесть, что \(u_\omega d\omega = u_\nu d\nu\), и следовательно, \(u_\omega = u_\nu \frac{d\nu}{d\omega} = \frac{1}{2\pi}u_\nu\). Необходимо также заменить в формуле \(\nu\) на \(\frac{1}{2\pi}\omega\). Кроме того, удобно ввести вместо постоянной Планка новую константу \(\hbar = \frac{1}{2\pi}h\). Тогда получаем: \[u_\omega = \frac{\hbar\omega^3}{\pi^2c^3} \frac{1}{e^{\hbar\omega/kT}-1}\] Константа \(\hbar\) получила название редуцированной постоянной Планка или постоянной Дирака, её значение по современным данным равно: \[\hbar = 1,054571800(13)\times 10^{-34}~\text{Дж}\cdot\text{с}\]
В прикладных исследованиях важным бывает также распределение не по частотам, а по длинам волнам \(\lambda=\frac{c}{\nu}\). Для этого распределения несложно получить следующее выражение: \[u_\lambda = \frac{8\pi hc}{\lambda^5} \frac{1}{e^{hc/\lambda kT}-1}\]
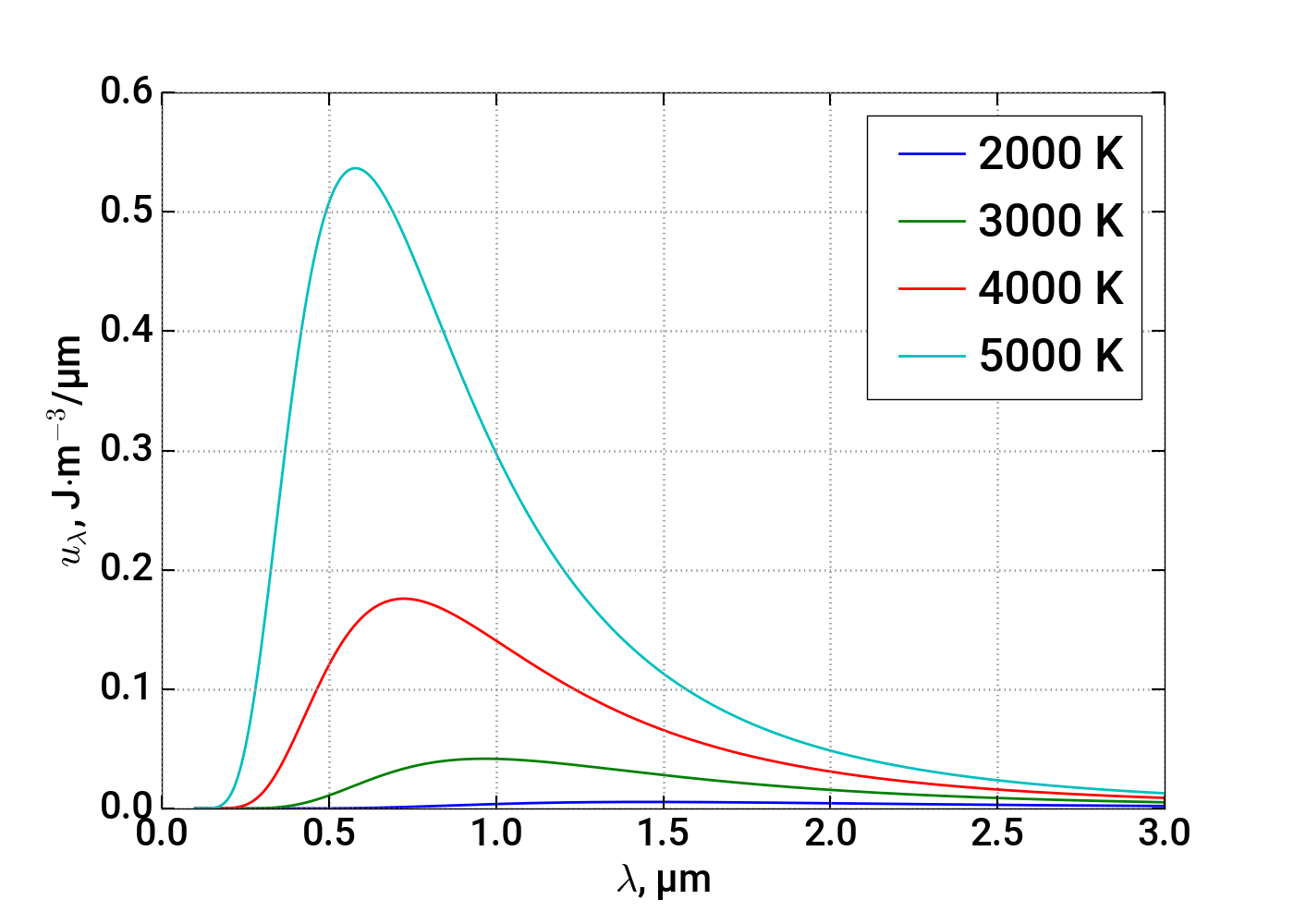
Можно показать, что в предельных случаях \(h\nu \ll kT\) и \(h\nu \gg kT\) формула Планка переходит в формулу Рэлея — Джинса и вторую формулу Вина соответственно. Кроме того, поскольку в процессе её вывода использован первый закон Вина, то она автоматически удовлетворяет также закону смещения Вина и закону Стефана — Больцмана.
Интересно, что сам Планк считал гипотезу квантования формальным предположением. Впоследствии, однако, именно она дала рост совершенно новым представлениям об устройстве мира вообще и микромира в частности, приведя к созданию в конце 1920-х годов последовательной квантовой теории.
3 Фотоны
3.1 Фотоэлектрический эффект
В 1887 году Генрих Герц обнаружил, что если отрицательный электрод искрового промежутка облучать ультрафиолетовым излучением, то это упрощает возникновение искры при подаче напряжения между электродами. Сам Герц на это большого внимания не обратил.
3.1.1 Законы фотоэффекта
Исследования показали, что сила фототока в вакуумном промежутке росла с ростом приложенного напряжения, но стремилась к некоторому значению (току насыщения), величина которого зависит от интенсивности излучения.
Систематическое исследование эффекта, проведённое Александром Григорьевичем Столетовым в 1888–1890 годах, показало, что сила тока насыщения при фотоэффекте пропорциональна интенсивности излучения. Это стало содержанием так называемого первого закона фотоэффекта.
Было также показано, что эффект обусловлен тем, что при облучении поверхности электрода с него удаляется отрицательный заряд. Физическую сущность этого заряда удалось, однако, понять только после открытия в 1897 году электрона. В своих экспериментах Джозеф Джон Томсон, а также Филипп Ленард в 1900 году показали, что покидающий электрод отрицательный заряд — это электроны.
Ленард также установил, что максимальная скорость, которую электроны приобретают при вылете из облучаемого тела, не зависит от интенсивности, а определяется только частотой излучения. Это наблюдение является содержанием так называемого второго закона фотоэффекта.
Кроме того, была обнаружена странная зависимость порога фотоэффекта (то есть, запирающего напряжения, при котором начинает течь фототок) от частоты излучения. Оказалось, что имеется некий порог частоты — так называемая «красная граница» — ниже которого фототок отсутствует вовсе, а выше этого порога запирающее напряжение прямо пропорционально частоте. Это так называемый третий закон фотоэффекта.
Хотя сам эффект фототока не противоречит классическим представлениям, его свойства не могут быть объяснены в рамках классической физики. Действительно, по классическим представлениям электроны вылетают из тела, приобретая энергию в поле излучения. При этом чем выше интенсивность излучения, тем выше должна была быть энергия электрона. Она же на практике зависит не от интенсивности, а от частоты. Кроме того, должна была бы существовать интенсивность, ниже которой ток должен прекращаться, чего также не наблюдалось. Невозможно было объяснить и наличие «красной границы» — в классической физике электрон может получить энергию от излучения любой частоты. И наконец, согласно классическим представлениям, электрону требуется некоторое время, чтобы набрать необходимую для покидания тела энергию, однако на практике фототок возникает практически сразу после начала освещения, то есть фотоэффект не обладает инерционностью.
3.1.2 Теория Эйнштейна
Решить проблему фотоэффекта удалось Альберту Эйнштейну в 1905 году. Формально именно за это ему была присуждена в 1921 году Нобелевская премия по физике. Для решения проблемы Эйнштейн воспользовался квантовой гипотезой Макса Планка, однако немного её расширил. Эйнштейн не просто предположил, что излучение поглощается и излучается квантами, но и выдвинул идею, что излучение и представляет собой поток таких квантов — то есть частиц света. Позднее эти частицы получили название фотонов. При этом вслед за Планком Эйнштейн постулировал, что энергия кванта света связана с его частотой по формуле \[E_\nu = h\nu\] Электрон приобретает энергию в результате поглощения одного фотона. Величина этой энергии, очевидно, равна: \[E^{\text{кин}} = h\nu - A_{\text{вых}}\] где величина \(A_{\text{вых}}\) получила название работы выхода и равна работе, которую необходимо затратить, чтобы вырвать электрон из тела. Приведённое выше уравнение называется уравнением Эйнштейна для фотоэффекта. Оно объясняет все три закона фотоэффекта:
- Плотность тока насыщения \(j\) пропорциональна максимальному количеству электронов \(dN_e\), которое можно вырвать с единичной площадки \(dS\) фотонами в единицу времени \(dt\): \[ j = en_ev = e\frac{dN_e}{vdtdS}v = e\frac{dN_e}{dtdS} \] Величина \(dN_e\) равна количеству фотонов, поглощаемых телом за тот же промежуток времени, и оно пропорционально количеству фотонов \(dN_\nu\), падающих на тело в единицу времени: \[j \sim e\frac{dN_\nu}{dtdS}\] С другой стороны, интенсивность излучения равна полной энергии всех фотонов, проходящих за время \(dt\) через площадку \(dS\): \[I = \frac{E_\nu dN_\nu}{dtdS}\] таким образом: \[j\sim I\] то есть ток насыщения пропорционален интенсивности, что и было продемонстрировано в экспериментах.
- Максимальная скорость вырываемых электронов определяется разностью между энергией одного фотона и работой выхода (скорость может оказаться меньше, если электрон, получив энергию от фотона, прежде чем вылететь наружу испытает столкновение с атомами тела): \[\frac{mv_{max}^2}{2} = h\nu - A_{\text{вых}}\] Таким образом, она не зависит от интенсивности излучения, а определяется только его частотой.
- И наконец, если частота излучения ниже \(\nu_0\) такой, что: \[h\nu_0 = A_{\text{вых}}\] то электрону, поглотившему фотон, не хватит энергии, чтобы покинуть тело. Таким образом для излучения, частота которого ниже \(\nu_0\), фототок будет отсутствовать. То есть \(\nu_0 = \frac{A_{\text{вых}}}{h}\) — это «красная граница» фотоэффекта.
- Поскольку процесс поглощения фотона мгновенен, то фотоэффект должен возникать сразу же после включения источника, то есть согласно теории Эйнштейна он является безынерционным.
Теория Эйнштейна была детально проверена в экспериментах Оуэна Ричардсона и Карла Комптона в 1912 году и Роберта Милликена в 1916 году. Они подтвердили справедливость теории, хотя, например, Милликен изначально затевал свои опыты в надежде опровергнуть Эйнштейна.
Из уравнения Эйнштейна несложно получить зависимость запирающего напряжения от частоты излучения: \[eV_{\text{з}} = E^{\text{кин}}_{max} = h\nu - A_{\text{вых}}\] \[V_{\text{з}} = \frac{h}{e}\nu - \phi_{\text{вых}}\] Величина \(\phi_{\text{вых}} = \frac{A_{\text{вых}}}{e}\) называется потенциалом выхода. Из сравнения полученной зависимости с экспериментом по наклону кривой можно вычислить постоянную Планка — это независимый способ её определения. Измерения показали, что в пределах погрешности она совпадает с методом, основанным на изучении теплового излучения.
3.2 Понятие фотона
Макс Планк и многие другие учёные полагали, что квантованность процесса поглощения и излучения является свойством вещества, но не электромагнитной волны. Эйштейн, однако, в своих рассуждениях считал, что это свойство самого излучения. То есть электромагнитные волны представляют собой совокупность неких квантов, порций, или, другими словами, частиц. Несмотря на то, что корпускулярная теория света была достаточно популярна до XVIII века (в частности, её придерживался Ньютон) работами Томаса Юнга и Огюстена Френеля в начале XIX века было показано, что свет дифрагирует и интерферирует, то есть является волной. Это представление было закреплено электромагнитной теорией Джеймса Максвелла в 1865 году. Таким образом, идея Эйнштейна о корпускулярности света в известной степени противоречила общепринятым на тот момент представлениям. По этой причине она не могла быть быстро принятой научным сообществом.
Сам Эйнштейн называл введёные им частицы света просто квантам света (нем. das Lichtquant). В 1926 году, однако, химиком Гилбертом Н. Льюисом им было дано название «фотоны» от греч. \(\varphi\omega\sigma\), «phos» («свет»). Это название и закрепилось в дальнейшем.
3.2.1 Энергия и импульс фотона
Существенным продвижением на пути признания фотонов объективно существующими объектами стали работы Эйнштейна 1909 и 1916 годов, в которых он показал, что как частицы они должны обладать определённым импульсом.
Действительно, поскольку фотон обладает энергией: \[E = h\nu\] то из специальной теории относительности для него справедливо равенство: \[\left(\frac{E}{c}\right)^2-p^2=m_0^2c^2\] где \(m_0\) — неизвестная нам масса фотона. Нам, однако, известно, что фотоны должны двигаться со скоростью света. Конечно, эта скорость не обязана, вообще говоря, совпадать со скоростью \(c\), фигурирующей в уравнениях теории относительности, однако, эксперименты показывают, что они совпадают с высокой точностью. Поэтому, записав релятивистское выражение для энергии фотона, мы получаем: \[E = \frac{m_0c^2}{\sqrt{1-v^2/c^2}}\] При условии, что \(v=c\), это выражение может дать результат, отличный от бесконечности, только если \(m_0=0\), то есть фотоны должно быть безмассовыми частицами. В этом случае получаем следующую связь между энергией и импульсом фотона: \[p = \frac{E}{c}\] и тогда импульс равен: \[p = \frac{h\nu}{c} = \frac{h}{2\pi}k = \hbar k\] где \(k\) — волновое число электромагнитной волны, квант которой мы рассматриваем.
Мы определили величину импульса, но не его направление. Чтобы узнать и направление тоже, мы можем воспользоваться аналогией. В теории относительности трёхмерным векторам соответствуют 4-вектора. Так, импульсу соответствует 4-импульс: \[\hat{p} = \left(\frac{E}{c}, \vec{p}\right)\] а волновому вектору — волновой 4-вектор: \[\hat{k} = \left(\frac{\omega}{c}, \vec{k}\right)\] Если мы сравним эти два выражения в приложении к фотону и его волне, то увидим, что их временная компонента отличается на множитель \(\hbar\), и на тот же множитель отличаются модули пространственных векторов. Поэтому естественно предположить, что между этими 4-векторами существует простая связь: \[\hat p = \hbar\hat k\] и следовательно обычный пространственный импульс фотона равен \[\vec p = \hbar\vec k\] Это предположение было впоследствии подтверждено и экспериментально.
3.3 Эффект Комптона
Несмотря на то, что Эйнштейн использовал понятие фотона как частицы света для доказательства теории фотоэффекта, эта идея настолько противоречила известным опытам по волновой природе света, что требовала более серьёзных доказательств. В принципе, фотоэффект мог быть объяснён и в рамках более консервативного предположения о том, что квантование — это свойство не самого излучения, а только процесса его взаимодействия с веществом. Поэтому было бы интересно найти процессы, в которых происходило взаимодействие фотона как частицы с другими известными частицами. Такими, как, например, электрон.
И такой процесс был обнаружен и объяснён в 1922–1923 годах американским физиком Артуром Комптоном. За это открытие он был награждён Нобелевской премией 1927 года.
Комптон проводил следующие исследования. У него имелась рентгеновская трубка, излучение которой пропускалось через систему диафрагм и посылалась на образцы исследуемых тел. Прошедшее через тело излучение регистрировалось специальным спектрометром, способным определять частоту излучения. Спектрометр был способен вращаться вокруг исследуемого тела, тем самым можно было снимать, как зависит спектр рассеянного излучения от угла наблюдения.
Оказалось, что при наблюдении под углом в спектре присутствовали два пика — один на исходной длине волны рентгеновского излучения, а второй — на смещённой в более длинноволновую часть спектра. При этом величина смещения увеличивалась с ростом угла рассеяния.
Этот эффект смещения длины волны рассеянного излучения, получивший название эффекта Комптона, получил своё теоретическое объяснение в рамках квантовой теории в работах самого Комптона, а также Петера Дебая.
Им удалось свести его к процессу столкновения частиц света — фотонов — со свободными электронами среды. Действительно, если рассмотреть этот процесс как упругий удар, то для него справедливы законы сохранения импульса и энергии: \[ \vec p_{\text{ф}} + \vec p_e = \vec p_{\text{ф}}^\prime + \vec p_e^\prime \\ \] \[ E_{\text{ф}} + E_e = E_{\text{ф}}^\prime + E_e^\prime \] где \(\vec p_{\text{ф}}, E_{\text{ф}}\) — импульс и энергия фотона до столкновения; \(\vec p_{\text{ф}}^\prime, E_{\text{ф}}^\prime\) — импульс и энергия фотона после столкновения; \(\vec p_e, E_e\) — импульс и энергия электрона до столкновения; \(\vec p_e^\prime, E_e^\prime\) — импульс и энергия электрона после столкновения. Обычно можно пренебречь энергией теплового движения электрона по сравнению с энергией фотона, и считать электрон изначально неподвижным: \(\vec p_e = 0\), \(E_e = m_ec^2\).
Выразим из закона сохранения импульса величину \(\vec p_e^\prime\) и найдём её квадрат: \[ \left(\vec p_e^\prime\right)^2 \equiv {p_e^\prime}^2 = \left( \vec p_{\text{ф}} - \vec p_{\text{ф}}^\prime\right)^2 = p_{\text{ф}}^2 + {p_{\text{ф}}^\prime}^2 - 2p_{\text{ф}}p_{\text{ф}}^\prime \cos\vartheta \] где мы ввели угол рассеяния \(\vartheta\) — то есть угол между направлениями распространения изначального и рассеянного фотонов.
Из закона сохранения энергии выразим \(E_e^\prime\) и найдём её квадрат: \[ {E_e^\prime}^2 = m_e^2c^4 + E_{\text{ф}}^2 + {E_{\text{ф}}^\prime}^2 - 2E_{\text{ф}}E_{\text{ф}}^\prime + 2m_ec^2(E_{\text{ф}}-E_{\text{ф}}^\prime) \] Учтём теперь связь между энергией и импульсом: \[ {E_e^\prime}^2 = m_e^2c^4 + {p_e^\prime}^2c^2 \\ \] \[ E_{\text{ф}} = p_{\text{ф}}c \\ \] \[ E_{\text{ф}}^\prime = p_{\text{ф}}^\prime c \] и совместим оба полученных выражения, исключив импульс электрона: \[ m_e^2c^4 + \left(p_{\text{ф}}^2 + {p_{\text{ф}}^\prime}^2 - 2p_{\text{ф}}p_{\text{ф}}^\prime \cos\vartheta\right) c^2 = m_e^2c^4 + p_{\text{ф}}^2c^2 + {p_{\text{ф}}^\prime}^2c^2 - 2p_{\text{ф}}p_{\text{ф}}^\prime c^2 + 2m_ec^3(p_{\text{ф}}-p_{\text{ф}}^\prime) \\ \] \[ 2p_{\text{ф}}p_{\text{ф}}^\prime c^2 \cos\vartheta = 2p_{\text{ф}}p_{\text{ф}}^\prime c^2 + 2m_ec(p_{\text{ф}}-p_{\text{ф}}^\prime) \\ \] \[ \frac{1}{p_{\text{ф}}^\prime} - \frac{1}{p_{\text{ф}}} = \frac{1 - \cos\vartheta}{m_ec} \] Это выражение может быть получено и из классических соображений, но чтобы вывести из него спектральные характеристики света, необходимо установить связь между импульсом фотона и его частотой и длиной волны. Эта связь, полученная нами выше, имеет, согласно Эйнштейну, вид \[ p = \hbar k = \hbar \frac{2\pi}{\lambda} = \frac{h}{\lambda}\] Таким образом, имеем: \[\lambda^\prime - \lambda = \left(1 - \cos\vartheta\right)\frac{h}{m_ec}\] Эта зависимость смещения рассеянной длины волны от угла рассеяния была подтверждена экспериментально. Её особенностями является, во-первых, то, что величина смещения не зависит от материала мишени, а во-вторых, то, что величина смещения не зависит от длины волны падающего излучения.
Величина \(\frac{h}{m_ec}\) носит название комптоновской длины волны \(\lambda_{\text{к}}\). Она характеризует ту частицу, на которой происходит рассеяние — в данном случае электрон. Аналогичную величину можно вычислить и для других заряженных частиц — протона и т. п. Для электрона комптоновская длина волны численно равна: \[ \lambda_{\text{к}} = 2,4263096 \cdot 10^{-12} \text{м} \] Часто также в расчётах полезно ввести редуцированную комптоновскую длину волны: \[ \rlap{-}\lambda_{\text{к}} = \frac{\lambda_{\text{к}}}{2\pi} = \frac{\hbar}{m_ec} \] Дополнительным доказательством того, что эффект Комптона объясняется рассмотренным элементарным взаимодействие фотона и электрона, является непосредственное наблюдение электронов отдачи (электронов, с которыми произошло столкновение), в камере Вильсона. Такие эксперименты были проведены вскоре после работ самого Комптона.
Рассмотренный выше эффект приводит к увеличению длины волны рассеянного излучения (уменьшению частоты). Это связано с тем, что электрон предполагался изначально покоящимся. Однако можно рассмотреть и рассеяние на движущемся элетроне. В этом случае длина волны рассеянного фотона может оказаться меньше, чем длина волны падающего излучения. То есть фотон увеличит свою энергию за счёт энергии электрона. Этот эффект называется обратным эффектом Комптона и может быть использован, например, для генерации излучения высокой частоты (рентгеновского и гамма-диапазонов).
4 Волновые свойства частиц
Наличие у света не только волновых, но и корпускулярных свойств поставило серьёзную проблему перед учёными начала XX века. К этой проблеме предлагались различные подходы, пытавшиеся в том числе свести всё к известным классическим представлениям о мире. Однако все они оказывались неудачными, и очень важным этапом в отказе от таких попыток стало открытие волновых свойств не только у света, но и у обычных частиц вещества.
4.1 Гипотеза де Бройля
Идея о том, что своеобразный дуализм свойств света — то, что называется корпускулярно-волновым дуализмом, — может быть присущ и частицами вещества, была выдвинута Луи де Бройлем в 1924 году. За свои работы в этой области де Бройль был награждён Нобелевской премией 1929 года. При этом им двигало стремление к наличию некой симметрии в природе.
Поскольку всякую электромагнитную волну мы вынуждены рассматривать и как поток частиц — фотонов, то Де Бройль предложил и наоборот приписать каждой известной частице некую волну, получившую название волны де Бройля. Например, с движущемся электроном ассоциируется некая монохроматическая волна вида \[ \psi = \psi_0 \exp\left\{{i\left(\vec k\vec r - \omega t\right)}\right\} \] Входящие в выражение для этой волны величины частоты \(\omega\) и волнового вектора \(\vec k\) де Бройль предложил связать с энергией и импульсом частицы аналогично связи, установленной для фотонов: \[ E = \hbar\omega \] \[ \vec p = \hbar \vec k \] где под \(E\) надо понимать ту энергию, которая входит в 4-вектор энергии-импульса \(\left(E/c, \vec p\right)\), то есть сумму энергии покоя частицы и её кинетической энергии.
Длина волны де Бройля связана с импульсом частицы соотношением \[ \lambda = \frac{2\pi}{k} = \frac{2\pi\hbar}{p} = \frac{h}{p} \] Рассмотрим свойства введённой волны. Вычислим вначале её фазовую скорость: \[ v_\text{ф} = \frac{\omega}{k} = \frac{E}{p} = \frac{\gamma mc^2}{\gamma mv} = \frac{c^2}{v} \] где \(\gamma = \left(1-v^2/c^2\right)^{-1/2}\) — гамма-фактор частицы. Как видим, фазовая скорость волны де Бройля всегда больше скорости света (за исключением частиц, движущихся со скоростью света, например, фотонов), это, однако, не противоречит теории относительности, поскольку известно, что фаза волны не может переносить информацию или энергию.
Физически более информативна групповая скорость волн. Вычислим её величину для волн де Бройля: \[ v_\text{гр} = \frac{d\omega}{dk} = \frac{dE}{dp} \] Рассмотрим связь между энергией и импульсом и продифференцируем её по импульсу: \[ E^2 = p^2c^2 + m^2c^4 \] \[ E\frac{dE}{dp} = pc^2 \] \[ \frac{dE}{dp} = \frac{pc^2}{E} = \frac{v}{c^2}c^2 = v \] где мы воспользовались найденным ранее выражением для величины \(E/p\). Из приведённых выкладок, видно, что групповая скорость волн де Бройля совпадает со скоростью частицы, что является аргументом в пользу правильности нашего предположения о виде волны.
4.2 Эксперименты по дифракции электронов
Окончательный ответ на вопрос, является ли предположение де Бройля верным, мог дать только эксперимент, в котором было бы показано, что частицы, например, электроны обладают волновыми свойствами.
Чтобы понять, возможно ли наблюдение волновых свойств электронов в эксперименте, оценим величину длины волны де Бройля \(\lambda = \frac{h}{p}\) в нерелятивистском случае (\(p = \sqrt{2m_eE}\)). Если энергию измерять в электрон-вольтах (то есть, оценивать её в эксперименте по ускоряющей разности потенциалов), получаем следующую численную оценку: \[ \lambda = \frac{1,225\ \text{нм}}{\sqrt{E[\text{эВ}]}} \] Таким образом для ускоряющего потенциала около 150 В длина волны де Бройля становится равной 1 ангстрему, то есть становится сравнимой с размерами атомов и расстоянием между ними в твердых телах. Это обстоятельство и может быть использовано для наблюдения, например, эффекта дифракции электронов.
Действительно, атомы в кристаллических телах образуют строго периодическую структуру, называемую кристаллической. В этой структуре всегда существуют параллельные плоскости, образованные атомами. Эти плоскости можно рассматривать как частично отражающие электроны поверхности. При этом на них должна наблюдаться дифракция аналогичная дифракции в тонких плёнках. Согласно условию Брэгга — Вульфа, условием максимума интенсивности является выполнение соотношения: \[ 2d\sin\varphi = n\lambda \] где \(d\) — расстояние между двумя соседними плоскостями, \(\varphi\) — угол скольжения Брэгга (угол между направлением распространения падающих электронов и кристаллической плоскостью), \(\lambda\) — длина волны де Бройля падающих электронов, \(n=1,2,3,\dots\) — порядок дифракции.
Интересно, что подобная угловая зависимость интенсивности рассеянных электронов наблюдалась Клинтоном Дэвиссоном и Кэнсманом ещё в 1921–1923 годах, но тогда она не была понята. Повторные эксперименты Дэвиссон провёл в 1926–1927 годах совместно с Лестером Джермером, уже зная о гипотезе де Бройля. В своих экспериментах он получил качественное согласие с теорией. Количественные расхождения были объяснены тем, что волны де Бройля преломляются в кристалле, что не учитывается при выводе условия Брэгга — Вульфа.
Приведённый выше метод наблюдения дифракции носит название метода Брэгга. Есть и другие способы, например, метод Дебая — Шеррера, в котором взаимодействие происходит с материалом, растёртым в порошок. При этом на детекторах, установленных вокруг облучаемого образца, изображение получается в виде колец. Расстояние между линиями одного и того же кольца позволяет найти брэгговские углы отражения. Этим методом дифракция электронов была впервые продемонстрирована Джорджем Томсоном.
За открытие явления дифракции электронов Дэвиссон и Томсон были награждены Нобелевской премией 1937 года.
Наконец, волновые свойства электронов объяснили и эффект Рамзауэра, открытый в 1920–1921 годах. Эффект заключается в аномально слабом рассеянии медленных электронов атомами нейтральных газов и не может быть объяснён классически. Связан он с тем, что медленные электроны испытывают дифракцию на атомах аналогичную дифракции света на круглом экране. При этом наблюдается эффект, аналогичный эффекту пятна Пуассона в оптике — увеличению интенсивности излучения позади экрана в области тени. Электрон как бы огибает атом, не испытывая рассеяния.
4.3 Корпускулярно-волновой дуализм
Гипотеза Эйнштейна о корпускулярности света и экспериментальное подтверждение наличия волновых свойств у электрона поставило учёных перед фактом того, что на микроуровне частицы существенно отличаются своими свойствами от привычных нам тел. Возникла концепция корпускулярно-волнового дуализма, согласно которой объекты микромира обладают одновременно и волновыми свойствами (испытывают дифракцию и интерференцию), и корпускулярными (поглощаются и излучаются фиксированными «порциями», взаимодействуют между собой как упругие шары). Наш эмпирический опыт, однако, не содержит подобных объектов, поэтому не существует точных аналогий, которыми можно было бы описать объекты микромира в привычных нам терминах. Они требуют принципиально нового подхода и нового математического аппарата. Эта необходимость и привела к созданию в 1920-х годах нового раздела физики — квантовой механики, давшей впоследствии начало и другим дисциплинам квантовой физики (квантовой термодинамики, квантовой электродинамики, квантовой теории поля).
Конечно, были попытки объединения корпускулярных и волновых свойств на основе каких-то классических моделей, но они оказались несостоятельными.
Например, одно время существовала точка зрения, что существуют только волны, а частицы — это локализованные пакеты этих волн. В частности, такую теорию пытался построить Эрвин Шрёдингер. Однако подобным теориям приходилось вводить дополнительные гипотезы, объясняющие, каким образом эти волновые пакеты не расплываются в пространстве при своём распространении в силу дифракции и дисперсии. Эти гипотезы, однако, или было невозможно проверить в эксперименте, или не подтверждались на опыте.
Противоположным мнением было существование только частиц. Волны при этом рассматривались как волны вещества (аналогично, например, акустическим волнам, носителем которых являются частицы вещества). Однако эксперименты по дифракции одиночных частиц (например, эксперименты В. А. Фабриканта по дифракции одиночных электронов, проведённые в 1949 году) показали, что волновыми свойствами обладают и одиночные частицы.
В итоге была сформулирована непротиворечивая интерпретация корпускулярно-волнового дуализма, известная как статистическая интерпретация Макса Борна. Согласно ей, объекты микромира являются частицами, которым соответствует также некоторая волна де Бройля. При этом интенсивность волны де Бройля \(|\psi|^2\) в данной точке пространства пропорциональна вероятности обнаружить в ней частицу.
Эта интерпретация была впоследствии распространена на обобщение понятия волны де Бройля — волновую функцию, и стала основой самой популярной интерпретации квантовой механики, известной как копенгагенская интерпретация.
4.4 Принцип неопределённости Гейзенберга
Одним из важных следствий волновой природы всех известных нам микрообъектов и связанным с ней корпускулярно-волнового дуализма является существование так называемого принципа неопределённости Гейзенберга.
Рассмотрим электрон в свободном пространстве. Мы знаем, что если он обладает определённым импульсом, то его волновые свойства описываются волной де Бройля. Однако волна де Бройля неограниченна в пространстве, что, очевидно, является нефизичной ситуацией. Можно ли придумать волновую функцию свободного электрона, локализованного в каком-либо конечном объёме пространства? Ответ, да. Мы можем сконструировать волновую функцию как сумму волн де Бройля с разными импульсами. Примером такой локализованной функции является пакет волн де Бройля, имеющих близкие частоты.
Как известно из физики волн, любой волновой импульс можно разложить в ряд Фурье, то есть представить в виде суммы (в предельном случае интеграла) монохроматических волн. Волны де Бройля как раз и являются монохроматическими, поэтому локализованный электрон может быть описан как пакет волн де Бройля: \[ \Psi(\vec r, t) = \int c(\vec k)e^{i\vec k\vec r - \omega (\vec k) t} d^3\vec r \] Из общих свойств преобразования Фурье известно, что если функция \(\Psi\) имеет, например, вдоль оси \(x\) характерный размер \(\Delta x\), а её Фурье-образ \(c(\vec k)\) — \(\Delta k_x\), то они должны удовлетворять неравенству \(\Delta x\Delta k_x > 2\pi\). Если мы перейдём от волнового числа к импульсу, то получим следующее соотношение: \[\Delta x\Delta p_x > h\] Это соотношение и выражает в математической форме принцип неопределённости Гейзенберга. Величины \(\Delta x\) и \(\Delta p_x\) можно понимать как неопределённость значений координаты и импульса частицы. Суть принципа заключается в том, что невозможно абсолютно точно одновременно задать координату и импульс (скорость) частицы. Действительно, если мы пытаемся уменьшить неопределённость положения частицы, уменьшая \(\Delta x\), принцип Гейзенберга неизбежно ведёт к увеличению неопределённости её импульса \(\Delta p_x\).
Из этого следует, что в микромире неправомерна даже обычная для классической физики постановка задачи о движении частицы, когда по начальным значениям координаты и скорости определяются их значения во все следующие моменты времени. Принцип неопределенности запрещает задать начальные условия так, как это делается в классической теории. Отсюда, в частности, следует, что у квантового микрообъекта не может быть определённой траектории.
Принцип неопределённости Гейзенберга можно применить и к процессу измерения положения или скорости частицы. В частности, чем точнее мы измеряем положение частицы, тем сильнее мы должны возмутить её импульс и тем неопределённее он становится. И здесь мы сталкиваемся с ещё одним важным отличием микромира от макромира. В классической физике всегда можно сделать сколь угодно точное измерение, которое окажет сколь угодно слабо воздействие на измеряемую системы, в то время как в квантовой физике это невозможно. Увеличение точности измерения ведёт к увеличению степени воздействия на измеряемую систему, и наоборот, уменьшение степени воздействия на квантовую систему ведёт к уменьшению точности измерения.
Примером может служить попытка определить положение электрона путём рассеяния на нём фотона. Поскольку точка рассеяния фотона не может быть локализована точнее, чем длина волны фотона, то для улучшения точности необходимо использовать всё более и более коротковолновые фотоны. Но с уменьшением длины волны фотона растёт его энергия и импульс, поэтому в процессе рассеяния растёт и импульс, приобретаемый электроном. При этом мы не можем контролировать направление этого импульса, поэтому растёт и наша неопределённость в его знании.
5 Теория атома Бора
5.1 Ранние представления о строении атомов
5.1.1 Исторические сведения
Представления об атомах как о неделимых частицах вещества восходят к древнегреческим и древнеиндийским философам. В частности, концепция атомизма была предложена Левкиппом и его учеником Демокритом. Исследования химиков в XVII–XVIII веках позволило сформулировать атомно-молекулярную теорию строения вещества, однако природа атомов и их строение оставались открытыми вопросами. Фактически, атомы считались просто кусочками вещества, не имевшими внутренней структуры.
Представления об атомах начали стремительно меняться в начале XX века. В 1897 году Джозеф Томсон установил, что катодные лучи являются потоком частиц, получивших позднее название электронов (само название «электрон» для неделимой единицы электрического заряда было введено электрохимиком Джорджем Стоуни в 1894 году). В 1904 году Томсон выдвигает гипотезу, что электроны входят в состав атомов, располагаясь в нём в облаке положительного заряда, равного по величине сумме зарядов электронов. Эта модель получила название модели атома Томсона или модели «пудинга с изюмом».
Альтернативная модель, предложенная также в 1904 году японским физиком Хантаро Нагаока, помещала весь положительный заряд атома в его центр, при этом электроны вращались в этой теории вокруг положительного заряда подобно кольцам Сатурна. Эта теория стала предвестником так называемых планетарных теорий строения атома.
5.1.2 Модель Резерфорда
Ключевым для становления представлений о строении атомов стал эксперимент, проведённый в лаборатории Эрнеста Резерфорда Гансом Гейгером и Эрнстом Марсденом в 1909 году. В этом эксперименте исследовалось рассеяние недавно открытых альфа-частиц при их прохождении через тонкую золотую фольгу.
Было известно, что альфа-частицы обладают положительным зарядом и относительно большой массой. В эксперименте неожиданно было обнаружено, что хотя подавляющее число альфа-частиц рассеивается на углы в пределах 1–3 градусов, небольшая их часть испытывает очень сильное рассеяние — вплоть до 150 градусов. Это поведение было невозможно объяснить в рамках теории Томсона, и в 1911 году Резерфорд пишет статью, в которой выдвигают свою теорию, во многом аналогичную планетарной теории Нагаока. Согласно Резерфорду атом состоит из малого по объёму положительно заряженного ядра и электронов, вращающихся вокруг ядра по орбитам. По оценкам Резерфорда, если размер атома должен составлять \(10^{-10}\) м, то размер ядра — около \(10^{-15}\)–\(10^{-14}\) м. При этом практически вся масса атома сосредоточена в ядре атома.
Модель Резерфорда, однако, имела фундаментальные проблемы, связанные с устойчивостью. Дело в том, что поскольку электрон вращается вокруг ядра, то он испытывает ускорение, которое должно приводить к излучению и потери энергии. Оценки показывали, что электрон должен был бы потерять всю свою энергию за относительное короткое время, то есть атомы Резерфорда не могли бы существовать достаточно долго.
5.2 Спектры атомов
Другая проблема модели Резерфорда была связана со спектром поглощения и излучения атомов.
К началу XX века было уже известно, что излучение нагретых тел содержит не только широкополосный тепловой спектр, но и набор узких линий или полос, расположение которых зависит от состава исследуемого тела. Для атомарных веществ наблюдался линейчатый спектр, вид которого определялся типом химического элемента, образующего вещество. При этом вид атомного спектра не зависит от того, каким образом мы сообщаем энергию атомам — за счёт теплового движения, путём пропускания электрических разрядов, проведения химических реакция или облучения светом.
Были также установлены эмпирические формулы для частот, на которых располагались линии атомных спектров. Эти формулы в 1908 году были объединены в так называемый комбинационный принцип Ритца. Согласно этому принципу, всё многообразие спектральных линий можно получить путём попарной комбинации т. н. спектральных термов: \[\frac{1}{\lambda} = T_{n_1}-T_{n_2}\] где \(n_1 < n_2\). Выражение для термов \(T_n\) зависит от вида атома. В простейшем случае водорода оно имеет вид \[T_n = \frac{R}{n^2},\ \ n=1,2,\dots\] где величина \(R = 109678,76(1)\ \text{см}^{-1}\) называется постоянной Ридберга.
Частные случаи комбинационного принципа носят название серий. Серия при \(n_1 = 1\) называется серией Лаймана. Она была открыта в 1906 году: \[\frac{1}{\lambda} = R\left(1-\frac{1}{n^2}\right),\ \ n=2,3,\dots\] Первые линии этой серии лежат в ультрафиолетовом диапазоне.
Серия при \(n_1 = 2\) называется серией Бальмера. Она была первой серией, для которой в 1885 году была получена общая формула: \[\frac{1}{\lambda} = R\left(\frac{1}{4}-\frac{1}{n^2}\right),\ \ n=3,4,\dots\] Её первые четыре линии лежат в видимом диапазоне и известны как \(H_\alpha, H_\beta, H_\gamma, H_\delta\) (читается как «аш-альфа», «аш-бета» и т. д.).
Серия при \(n_1=3\) была предсказана Ритцем на основе его принципа и открыта Фридрихом Пашеном в том же 1908 году. Она носит название серии Пашена.
Таким образом, в спектре водорода максимальной длиной волны обладает первая линия серии Лаймана \(L_\alpha\) (\(n_1=1\), \(n_2=2\)). Её величина составляет 121,56 нм — это так называемая резонансная линия водорода, она, в частности, используется в астрономии для обнаружения атомарного водорода.
Для каждой серии имеется также граница или предел серии — значение длины волны, к которой стремится серия при \(n\to\infty\). Например, для серии Бальмера \(\lambda_\infty = 364,47\) нм.
Следует отметить, что структура атомных спектров не могла быть объяснена с точки зрения классической физики. Излучение является следствием ускоренного движения частиц, поэтому линейчатость спектра указывает на то, что частицы вещества должны двигаться по каким-то вполне определённым орбитам, выбор которых сложно объяснить из классических представлений. Но, более того, даже если мы зафиксируем орбиту, должно присутствовать излучение не только на основной частоте, но и на всех её гармониках — обертонах. То есть спектр должен был бы разбиваться на серии, в которых линии расположены на равном расстоянии друг от друга, тогда как в реальности таких серий не существует.
5.3 Полуклассическая модель атома Бора
Решить часть проблем строения атома и его спектральных свойств удалось ученику Эрнеста Резерфорда Нильсу Бору, который сформулировал новую теорию атома в 1913 году.
Теория Бора основана на двух постулатах:
- Атом может находиться только в особых, стационарных, состояниях, каждому из которых отвечает определённая энергия. В стационарном состоянии атом не излучает электромагнитных волн.
- Излучение и поглощение энергии атомом происходит при скачкообразном переходе из одного стационарного состояния в другое, при этом частота поглощённого/излучённого кванта излучения при переходе из состояния \(n\) в состояние \(m\) определяется следующим соотношением: \[ \nu = \frac{E_n - E_m}{h} \]
Энергия стационарных состояний определяется так называемым правилом квантования.
5.3.1 Теория Бора водородоподобных атомов
Рассмотрим вслед за Бором приложение его теории к так называемым водородоподобным атомам, то есть атомам, на орбите которых имеется только один электрон. Простейшим примером таких атомов является собственно водород, а также его изотопы. Другие примеры — это ионы \(\text{He}^{+1}\), \(\text{Li}^{+2}\) и т. д.
Бор предположил, что электрон в таких атомах двигается вокруг ядра по круговым орбитам, и при этом устойчивы только такие орбиты, на которых момент импульса \(L\) электрона равен целому числу постоянных Планка: \[ L = n\hbar,\ \ n=1,2,3,\dots \]
Эти постулаты объясняют комбинационный принцип Ритца и позволяют выразить постоянную Ридберга через фундаментальные константы. Покажем это.
Второй закон Ньютона, записанный для электрона, двигающегося вокруг ядра, имеющего заряд \(+Ze\) (\(Z=1,2,3,\dots\)), даёт: \[ m_e\frac{v^2}{r} = \frac{Ze^2}{4\pi\varepsilon_0r^2} \] где \(r\) — радиус орбиты, \(v\) — орбитальная скорость электрона. Выразим скорость электрона через его момент импульса, воспользовавшись соотношением \(L = mvr\), и выразим радиус орбиты: \[ r = \frac{4\pi\varepsilon_0L^2}{m_eZe^2} \] Согласно Бору, \(L=n\hbar\), и следовательно: \[ r_n = \frac{4\pi\varepsilon_0\hbar^2}{m_eZe^2}n^2 \] Радиус первой орбиты атома водорода (так называемый боровский радиус: \(n=1, Z=1\)) равен: \[ r_B = \frac{4\pi\varepsilon_0\hbar^2}{m_ee^2} = 0,529\cdot 10^{-10}\ \text{м} \] Найдём полную энергию электрона: \[ E_n = \frac{1}{2}m_ev^2 - \frac{Ze^2}{4\pi\varepsilon_0r_n} = - \frac{1}{2}\frac{Ze^2}{4\pi\varepsilon_0r_n} \] Или подставляя \(r_n\): \[ E_n = - \frac{m_eZ^2e^4}{32\pi^2\varepsilon_0^2\hbar^2}\frac{1}{n^2} \] учитывая, что, согласно постулатам Бора \[ \frac{1}{\lambda} = \frac{\nu}{c} = \frac{E_n - E_m}{hc} \] мы получаем комбинационный принцип Ритца со следующей связью между термами и энергиями атома Бора в случае водорода: \[ T_n = \frac{E_n}{hc} = \frac{me^4}{64\pi^3\varepsilon_0^2\hbar^3c}\frac{1}{n^2} \] Таким образом, мы нашли и выражение для постоянной Ридберга: \[ R_\text{теор} = \frac{me^4}{64\pi^3\varepsilon_0^2\hbar^3c} = \frac{me^4}{8\varepsilon_0^2h^3c} = 109737\ \text{см}^{-1} \] Отличие полученного значения от экспериментального главным образом объясняется тем, что мы пренебрегли массой ядра. Если её учесть, то получим: \(R = \frac{R_\text{теор}}{1+m/M} = 109677,6\ \text{см}^{-1}\), что практически совпадает с экспериментальным значением. Дальнейшее уточнение теоретического значения возможно при учёте релятивистских эффектов.
5.3.2 Связь теории Бора с гипотезой де Бройля
Отметим, что между гипотезой Бора о квантовании момента импульса электрона в атоме и выдвинутой позже гипотезой де Бройля о существовании волны, связанной с электроном, существует определённая связь. Заключается она в следующем. Выразим момент импульса электрона, двигающегося по круговой орбите, через его скорость: \[ L = mvr \] Согласно де Бройлю, электрону, двигающемуся со скоростью \(v\), соответствует волна, имеющая длину волны равную: \[ \lambda = \frac{h}{mv} \] Тогда условие Бора \[ L = n\hbar \] приводит к следующему равенству: \[ n\lambda = 2\pi r \] Это равенство имеет простой физический смысл: возможны только такие орбиты, на которых укладывается целое число длин волн де Бройля. Другими словами, стационарны только такие орбиты, на которых волны де Бройля являются стоячими.
5.3.3 Достоинства и недостатки теории Бора
Теория Бора имела большое значение, поскольку не только объяснила линейчатость атомных спектров, но и подошла к объяснению внутриатомных процессов с принципиально новых позиций, став первой полуквантовой теорией атома. Гипотезы о существовании стационарных состояний и скачкообразных переходов между ними сделали прорыв в понимании строения вещества на микроуровне.
Теория Бора имела и определённую предсказательную силу. Например, она предсказывала, как должен был выглядеть спектр однократно ионизованного гелия. Действительно, по своей структуре \(\text{He}^+\) отличается от атома водорода только массой и зарядом ядра, поэтому его спектр должен определяться термами, отличающимися от водородных в \(Z^2 = 4\) раз: \[ T_n = \frac{me^4}{16\pi^3\varepsilon_0^2\hbar^3c}\frac{1}{n^2} = \frac{4R}{n^2} \] Интересно, что ещё в 1887 году линии, порождаемые такими термами, были обнаружены Пикерингом в спектрах звёзд. Таким образом, теория Бора объяснила так называемую серию Пикеринга, которая до этого не имела удовлетворительного объяснения.
Однако теория Бора была логически несовершенна, не являясь ни классической, ни квантовой. Гипотезы Бора не имели никакого более глубокого объяснения. Кроме того, теория не могла предсказать интенсивность спектральных линий, и даже в строении спектра была справедлива только для водорода и водородоподобных атомов, то есть атомов с одним электроном. Для многоэлектронных атомов она даёт неправильные результаты. Требовалось создание и развитие совершенно новой общей теории микромира — квантовой механики.
6 Введение в аппарат физики микрообъектов
6.1 Уравнение Шрёдингера
Трудности теории атома Бора были связаны с тем, что она не являлась полностью классической. Постулируя квантованность момента импульса электрона в атоме, она описывала движение электрона классически. Чтобы построить полностью квантовую теорию атома, необходимо решать уравнения, описывающие квантовое движение электрона. Такое уравнение было впервые получено Эрвином Шрёдингером в 1925 году (опубликовано в 1926 году).
Толчком к написанию уравнения стала гипотеза де Бройля о волновых свойствах электронов и других частиц. Введённая им волна де Бройля, однако, описывала частицы во вполне определённом состоянии — в свободном пространстве и с постоянными импульсом и энергией. Шрёдингер попытался придумать уравнение, которое бы могло описать эволюцию волн, аналогичных волнам де Бройля, но описывающих частицы в произвольных потенциалах и с изменяющимися импульсом и энергией.
Уравнение Шрёдингера не может быть строго выведено из более фундаментальных представлений и постулируется, однако его вид можно попробовать угадать. Во-первых, это уравнение должно быть волновым, а во-вторых, ему должны удовлетворять волны де Бройля: \[ \Psi = \Psi_0 e^{i\left(\vec k\vec r - \omega t\right)} \] Причём \(\vec k\) и \(\omega\) здесь связаны с импульсом и кинетической энергией частицы: \(\vec p = \hbar\vec k\), \(E=\hbar\omega\). Поскольку между ними существует связь \(E=p^2/2m\), то должно быть справедливо и равенство \(\omega = k^2\hbar/2m\). Попробуем воспользоваться этим равенством, чтобы составить уравнение Шрёдингера. Для этого возьмём от волны де Бройля вторые производные по координатам и первую производную по времени: \[ \nabla^2\Psi\equiv\Delta\Psi=-k^2\Psi \] \[ \frac{\partial\Psi}{\partial t} = -i\omega\Psi \] В правых частях этих соотношений стоят нужные нам \(k^2\) и \(\omega\), приравняем их: \[ i\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\Delta\Psi \] Это уравнение является волновым. Его аналог в классической физике описывает распространение огибающей группы волн в квазиоптическом приближении. В квантовой физике оно называется уравнением Шрёдингера в отсутствие силовых полей.
Нам, однако, требуется уравнение, которое описывало бы движение электрона и в присутствии внешних сил. Чтобы его получить, ограничимся рассмотрением только потенциальных сил, описываемых функцией потенциальной энергии \(U(\vec r)\). Мы можем заметить, что правая часть уравнения Шрёдингера в отсутствие полей может быть записана как: \[ -\frac{\hbar^2}{2m}\Delta\Psi = \frac{p^2}{2m}\Psi \] Поэтому логично прибавить к имеющейся здесь кинетической энергии ещё и потенциальную. Тогда уравнение Шрёдингера в потенциальных полях примет вид: \[ i\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\Delta\Psi + U(\vec r)\Psi \] Подчеркнём ещё раз, что проделанный выше вывод не может считаться сколь-нибудь строгим. Это просто попытка угадать уравнение, вид которого мы теперь можем постулировать и верность которого необходимо проверять в эксперименте. Оказалось, что уравнение Шрёдингера в приведённой форме с очень высокой точностью описывает все известные на данный момент квантовые эффекты, не выходящие за рамки нерелятивистского приближения (несложно показать, что уравнение Шрёдингера не является инвариантным относительно преобразований Лоренца и потому не может претендовать на описание релятивистских процессов).
Важно отметить также, что вид потенциальной энергии, использованный нами в уравнении Шрёдингера, неявно подразумевает наличие корпускулярно-волнового дуализма. Действительно, если бы мы хотели записать потенциальную энергию распределённого в пространстве объекта (волны), то мы должны были проинтегрировать потенциальную энергию частей этого объекта по занимаемому им объёму. Здесь, однако, мы используем локальное значение потенциальной функции в некой точке \(\vec r\).
6.1.1 Свойства уравнения Шрёдингера
Уравнение Шрёдингера является комплекснозначным дифференциальным уравнение в частных производных первого порядка относительно производной во времени. Представляя собой уравнение движения частицы, оно является аналогом второго закона Ньютона, однако имеет совершенно другие свойства. В частности, поскольку это уравнение первого порядка, для его решения необходимо задание в начальный момент только функции \(\Psi(\vec r, 0)\), но не её производных. Кроме того, в силу комплекснозначности уравнение Шрёдингера, по сути, является не одним уравнением, а двумя связанными между собой (для действительной и мнимой части или для амплитуды и фазы).
Важным свойством уравнения Шрёдингера является его линейность: если функции \(\Psi_1\) и \(\Psi_2\) являются его решениями, то и функция \(\Phi = c_1\Psi_1 + c_2\Psi_2\) (где \(c_1\) и \(c_2\) — произвольные комплексные константы) тоже является решением. Это свойство называется также принципом суперпозиции. Отсюда, в частности, следует, что если функция \(\Psi\) является решением, то и функция \(c\Psi\) тоже является решением. Это обстоятельство позволяет проводить нормировку функции \(\Psi\) удобным для решения задачи образом.
Если задача ограничена в пространстве, то обычно для выбора нормировки используют тот факт, что физический смысл функции \(\Psi\) трактуется статистически: \(|\Psi|^2(\vec r) = \Psi(\vec r)\Psi^*(\vec r)\) (звёздочка означает взятие комплексного сопряжения) равна вероятности обнаружить частицу в точке \(\vec r\). Поскольку вероятность обнаружить частицу хотя бы где-то всегда равна единице, то условие нормировки обычно записывают как: \[ \int\limits_V \Psi\Psi^* dV = 1 \] где интегрирование понимается по всему доступному частице объёму.
Введённая таким образом нормировка не годится, однако, для задач, решаемых в неограниченном пространстве, так что нормировочный интеграл расходится. Такая постановка задачи, однако, является идеализированной и не обладает непосредственным физическим смыслом, поэтому выбор нормировки в ней не должен влиять на конечный результат, то есть она может быть выбрана произвольно.
6.1.2 Стационарное уравнение Шрёдингера
Уравнение Шрёдингера описывает всё многообразие динамики квантовых частиц. Однако среди всевозможных его решений особый интерес представляют решения, являющиеся стационарными. Локальная амплитуда таких решений не меняется во времени, поэтому они могут быть представлены в следующем виде: \[ \Psi (\vec r, t) = \psi(\vec r) e^{-i\omega t} \] Подставляя это решение в уравнение Шрёдингера, получаем: \[ \hbar\omega\psi = \left[ -\frac{\hbar^2}{2m}\Delta + U(\vec r) \right]\psi \] По аналогии с фотонами и волной де Бройля величину \(\hbar\omega\) мы можем трактовать как энергию частицы \(E\). Таким образом, в стационарных состояниях энергия частицы является постоянной во времени, а пространственная компонента её волновой функции подчиняется следующему уравнению: \[ -\frac{\hbar^2}{2m}\Delta\psi + U(\vec r)\psi = E\psi \] Это уравнение носит название стационарного уравнения Шрёдингера, но нередко называется и просто уравнением Шрёдингера, если из контекста его невозможно перепутать с полным уравнением Шрёдингера.
Стационарное уравнение Шрёдингера решает проблему квантования состояний частиц. Если в теории Бора квантованность момента импульса электрона постулировалась, то в рамках уравнения Шрёдингера она объясняется тем, что электрон может относительно долго находиться только в стационарных состояниях, но в силу того, что стационарное уравнение Шрёдингера вкупе с граничными условиями является задачей Штурма — Лиувилля, оно имеет решение только для дискретного набора собственных чисел \(E_n\), которые и образуют энергетический спектр частицы. Исключение составляют случаи, когда движение частицы ничем не ограниченно. В этом случае дополнительные условия на значения энергии не накладываются, и частица обладает непрерывным энергетическим спектром. Примером такой ситуации может быть частица в свободном пространстве, описываемая в стационарном состоянии волнами де Бройля.
6.1.3 Свойства волновой функции
Чтобы искать решения уравнения Шрёдингера, нам необходимо наложить на волновую функцию определённые ограничения. Помимо уже упоминавшегося условия нормировки, постулируется, что волновая функция должна быть непрерывной, однозначной и конечной. Кроме того, непрерывными и конечными, за исключением особых точек, должны быть и все первые пространственные производные волновой функции \(\nabla\Psi\).
6.2 Уравнение Шрёдингера в потенциальных ямах
Важным частным случаем потенциальных сил являются так называемые потенциальные ямы. Рассмотрим достаточно общие свойства решений уравнения Шрёдингера в них. Пусть потенциал задан достаточно гладкой функцией, обращающейся в нуль на бесконечности и всюду неположительной. Для простоты будем считать её одномерной. Будем интересоваться только стационарными решениями. Запишем стационарное уравнение Шрёдингера в следующем виде: \[ \frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2} + (E-U(x))\psi = 0 \] Энергия системы \(E\) является параметром этой задачи, в зависимости от которой и будем искать решения.
Отметим, что все коэффициенты уравнения вещественны, поэтому и решения будем искать в вещественном виде (умножение найденного решения на комплексную константу даст тоже решение, но физически это будет то же самое решение).
Рассмотрим теперь отдельно случаи положительной и отрицательной энергии системы (относительно бесконечности, на которой мы считаем, что потенциальная энергия равна нулю).
6.2.1 \(E < 0\)
В этом случае имеются области пространства, в которых \(U(x) > E\). С классической точки зрения, нахождение системы в этих областях запрещено. Однако это не так в квантовой физике. Дело в том, что если бы системе было запрещено находиться в этих областях, то в них выполнялось тождественное равенство \(\psi = \frac{d\psi}{dx} = 0\). Но в силу условия непрерывности волновой функции и её производной (мы рассматриваем достаточно гладкие потенциалы) это условие справедливо и в так называемых точках поворотах, определяемых условием \(U(x_i) = E\). Поскольку решаемое нами уравнение второго порядка, то это привело бы к тому, что волновая функция \(\psi\) была тождественно равна нулю во всём пространстве, в том числе и там, где \(U(x) < E\).
Таким образом, мы приходим к выводу, что должна существовать ненулевая вероятность обнаружить при измерении систему и в точках, в которых \(U(x) > E\). Это одно из проявлений волновой природы квантовых систем.
Рассмотрим асимптотическое поведение волновой функции на бесконечности (\(x\to\pm\infty\)). В силу того, что по условию \(\lim\limits_{x\to\pm\infty} U(x) = 0\), а \(E < 0\), удобно ввести новый параметр \[\alpha = \sqrt{-\frac{2mE}{\hbar^2}}\] Тогда наше уравнение примет вид \[ \frac{d^2\psi}{dx^2} - \alpha^2\psi = 0 \] Оно имеет два решения: \(\psi_{-} = c_{-}e^{-\alpha x}\) и \(\psi_+ = c_+e^{\alpha x}\). При этом \(\psi_{-}\) расходится при \(x\to-\infty\) и \(\psi_{+}\) расходится при \(x\to+\infty\), поэтому в соответствующих асимптотиках они нефизичны.
Пусть теперь общее решение уравнения при \(x<0\) равно \(\psi_1 (x)\) и \(\psi_1 \to \psi_{+}\) при \(x\to-\infty\), а при \(x>0\) — \(\psi_2 (x)\) и \(\psi_2 \to \psi_{-}\) при \(x\to+\infty\). Тогда для нахождения полного решения нам необходимо «сшить» решения \(\psi_1\) и \(\psi_2\) в точке \(x=0\). Для этого наложим на них условия непрерывности: \[ \psi_1(0) = \psi_2(0) \] \[ \frac{d\psi_1}{dx}(0) = \frac{d\psi_2}{dx}(0) \] Это система относительно констант \(c_1\) и \(c_2\), которая имеет решение, только если её детерминант равен нулю. Детерминант системы зависит от значения \(E\), и следовательно, мы будем иметь некий дискретный набор значений \(E_n\), для которых он равен нулю. Это и будут стационарные уровни энергии нашей квантовой системы. Этим значениям соответствует дискретный набор стационарных решений \(\psi_n (x)\).
Отметим, что если потенциальная функция имеет глобальный минимум, в котором она равна \(U_{min}\), то при \(E = U_{min}\) система никогда не будет иметь решения. Математически это следует из того факта, что в этом случае вторая производная \(\psi^{\prime\prime} = \alpha^2\psi\) должна быть всюду (за исключение единственной точки минимума потенциала) положительна, что вкупе с требованием равенства нулю функции \(\psi\) на обеих бесконечностях, делает невозможным удовлетворение условия непрерывности первой производной (она также должна быть равна нулю в обеих бесконечностях, но при этом она всюду убывает).
6.2.2 \(E > 0\)
В этом случае нет областей, где \(U(x) > E\), и асимпотики волновой функции являются решением уравнения \[ \frac{d^2\psi}{dx^2} + \beta^2\psi = 0 \] где \[\beta^2 = \sqrt{\frac{2mE}{\hbar^2}}\] Решения этого уравнения представляют собой гармонические функции \(c_1\cos\beta x\) и \(c_2\sin\beta x\). Эти функции конечны на бесконечности, и потому повторяя рассуждения, приведённые выше для случая \(E < 0\), мы получим два уравнения, связывающие \(\psi_1\) и \(\psi_2\) в точке \(x=0\), и 4 неизвестные константы. Такая система будет иметь решение для любых значений \(E\), следовательно, система будет обладать непрерывным (сплошным) спектром энергий.
6.2.3 Квантование гармонического осциллятора
В качестве важного примера потенциальных ям рассмотрим задачу о квантовании одномерного гармонического осциллятора. Напомню, что под квантованием понимается определение допустимых (стационарных) значений энергии и соответствующих им волновых функций.
Потенциальная энергия гармонического осциллятора имеет вид \(U(x) = \frac{1}{2}m\omega^2x^2\), где \(\omega\) в классическом случае представляет собой круговую частоту колебаний осциллятора.
Квантование системы производится путём решения стационарного уравнения Шрёдингера: \[ -\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2} +\frac{1}{2}m\omega^2x^2\psi = E\psi \] Введём безразмерные переменные \[ \lambda = \frac{2E}{\hbar\omega} \] \[ \xi = x\sqrt{\frac{m\omega}{\hbar}} \] Получаем: \[ -\frac{d^2\psi}{d\xi^2} +\xi^2\psi = \lambda\psi \] \(\lambda\) является параметром нашей задачи, зафиксируем его и будем искать решение в виде \[\psi = e^{\alpha\xi^2}\] Найдём производные: \[ \frac{d\psi}{d\xi} = 2\alpha\xi e^{\alpha\xi^2} = 2\alpha\xi\psi \] \[ \frac{d^2\psi}{d\xi^2} = 2\alpha\psi + 2\alpha\xi\frac{d\psi}{d\xi} = \left(4\alpha^2\xi^2 + 2\alpha\right)\psi \] Подставим найденные производные в стационарное уравнение Шрёдингера: \[ -\left(4\alpha^2\xi^2 + 2\alpha\right)\psi + \xi^2\psi = \lambda\psi \] \[ -\left(1 - 4\alpha^2\right)\xi^2 - 2\alpha = \lambda \] Это уравнение должно иметь решение при любых \(\xi\), следовательно, должны быть равны нулю все коэффициенты при разных степенях \(\xi\): \[ 1-4\alpha^2 = 0 \] \[ -2\alpha = \lambda \] Эта система относительно \(\alpha\) имеет два корня \(\alpha_{\pm} = \pm\frac{1}{2}\), которым соответствуют значения параметра \(\lambda_{\pm} = \mp 1\). Решение \(\alpha_+\), однако, отвечает нефизичному случаю неограниченного роста функции \(\psi\) в пределах обеих бесконечностей. Таким образом, остаётся только решение \(\alpha_-\), которому соответствует волновая функция \[\psi = e^{-\frac{\xi^2}{2}}\] и энергия \[E = \frac{\lambda_-}{2}\hbar\omega = \frac{\hbar\omega}{2}\] Найденное нами решение отвечает основному состоянию гармонического осциллятора, то есть состоянию с наименьшей возможной энергией.
Чтобы показать это и найти все остальные состояния и их энергии, представим решение исходного уравнения в виде \[ \psi = f(\xi)e^{-\frac{\xi^2}{2}} \] где \(f(\xi)\) — некая функция, которую нам необходимо найти. Отметим, что такое представление никак не ограничивает искомое решение, а просто позволяет свести задачу к более простому уравнению. Действительно, для функции \(f(\xi)\) имеем: \[ f^{\prime\prime} - 2\xi f^{\prime} + (\lambda - 1)f = 0 \] Разложим \(f(\xi)\) в ряд: \[ f(\xi) = a_0 + a_1\xi + a_2\xi^2 + \dots \] Получаем: \[ \sum\limits_{k=2}^{\infty}k(k-1)a_k\xi^{k-2} - 2\xi\sum\limits_{k=1}^{\infty}ka_k\xi^{k-1} + (\lambda-1)\sum\limits_{k=0}^{\infty}a_k\xi^k = 0 \] \[ \sum\limits_{k=0}^{\infty}(k+2)(k+1)a_{k+2}\xi^k - 2\sum\limits_{k=1}^{\infty}ka_k\xi^k + (\lambda-1)\sum\limits_{k=0}^{\infty}a_k\xi^k = 0 \] Это уравнение должно иметь решение при любых \(\xi\), поэтому мы можем приравнять нулю коэффициенты при каждой из степеней \(\xi\). Получаем (для всех \(k\), кроме \(k=0\)): \[ a_{k+2}(k+2)(k+1) - 2ka_k + (\lambda - 1)a_k = 0 \] \[ \frac{a_{k+2}}{a_k} = \frac{2k - \lambda + 1}{(k+2)(k+1)} \] Рассмотрим поведение коэффициентов полученного ряда при больших \(k\): \[ \frac{a_{k+2}}{a_k} \to \frac{2}{k} \] Если сравнить это поведение с поведением коэффициентов разложения в аналогичный ряд функции \(e^{\xi^2}\): \[ e^{\xi^2} = \sum\limits_{k=0}^{\infty}\beta_{k}\xi^{k} = \sum\limits_{n=1}^{\infty}\beta_{2n}\xi^{2n} = \sum\limits_{n=1}^{\infty}\frac{1}{n!}\xi^{2n} \\ \frac{\beta_{k+2}}{\beta_k} = \frac{(k/2)!}{(k/2+1)!} \to \frac{2}{k} \] то мы видим совершенно одинаковую асимптотику. Это означает, что при достаточно больших \(\xi^2\), когда начинают доминировать большие члены ряда, наше решение \(f(\xi)\) асимптотически стремится к \(e^{\xi^2}\). Это, однако, противоречит физическому смыслу волновой функции, которая в этом случае тоже расходится: \(\psi(\xi) = f(\xi)e^{-\xi^2/2} \to e^{\xi^2/2}\).
Существует, однако, дискретный набор параметров \(\lambda\), при которых решение не расходится. Это такие \(\lambda\), при которых рассмотренный нами ряд обрывается на одном из членов. Условие обрыва ряда на \(k\)-ом члене выглядит как: \[ 2k - \lambda + 1 = 0 \] В этом случае \(a_{k+2}\) и все остальные члены ряда тождественно равны нулю, функция \(f(\xi)\) представляет собой полином, а функция \(\psi(\xi) = f(\xi)e^{-\xi^2/2}\) стремится на бесконечности к нулю. Отсюда получаем спектр собственных значений рассматриваемой задачи: \[\lambda_n = 2n + 1, n =0, 1, 2, \dots\] Соответствующий спектр энергии: \[E_n = \hbar\omega\left(n + \frac{1}{2}\right)\] Собственные функции \(f(\xi)\) представляют собой многочлены, носящие название многочленов Чебышева: \[f_n(\xi) = P_n(\xi)\] Собственные волновые функции в стационарных состояниях имеют вид: \[\psi_n(\xi) = P_n(\xi)e^{-\xi^2/2}\] Первые многочлены Чебышева имеют вид: \[ P_1(\xi) = a_1\xi \] \[ P_2(\xi) = a_2\left(\xi^2-\frac{1}{2}\right) \] \[ P_3(\xi) = a_3\left(\xi^3-\frac{3}{2}\xi\right) \] \[ P_4(\xi) = a_4\left(\xi^4-3\xi^2+\frac{3}{4}\right) \] Отметим некоторые особенности полученных решений, характерные также и для других задач в потенциальных ямах. Во-первых, в состоянии с наименьшей энергией энергия системы не равна нулю. Во-вторых, чем выше энергия стационарного состояния, тем больше пересечений с нулём имеет волновая функция, число таких пересечений равно порядковому номеру стационарного состояния начиная с самого нижнего, которому приписывается номер 0.
Уникальная особенность спектра энергий гармонического осциллятора, несвойственная другим системам, заключается в его эквидистантности — разница в энергии между соседними состояниями постоянна и равна \(\hbar\omega\), то есть гармонический осциллятор может терять и приобретать энергию только квантами, пропорциональными \(\hbar\omega\). Если такой осциллятор взаимодействует с электромагнитным полем, то он будет испускать и поглощать излучение только на частоте \(\omega\) и её гармониках \(n\omega, n = 2,3,4,\dots\)
6.3 Проникновение частицы в запрещённую область
Остановимся немного подробнее на явлении проникновения волновой функции в область, где полная энергия частицы \(E\) меньше потенциальной \(U(x)\). Как объяснить тот факт, что мы можем обнаружить частицу в этой области? Ведь, казалось бы, это означает, что её кинетическая энергия отрицательна, а импульс, следовательно, — мнимый. Чтобы разрешить этот парадокс, необходимо ещё раз вспомнить, что процесс измерения нарушает состояние измеряемой системы. Действительно, \(E\) — это энергия стационарного состояния. Чтобы измерить положение частицы, мы должны произвести то или иное взаимодействие с ней. Например, чтобы измерить положение электрона, его необходимо облучить фотоном. При этом длина волны фотона будет определять точность или, другими словами, неопределённость обнаружения электрона.
Если мы посмотрим на то, как устроена волновая функция в запрещённой зоне, то увидим, что она экспоненциально спадает с характерным масштабом спадания: \[ d = \frac{1}{\alpha} = \frac{\hbar}{\sqrt{2m(U-E)}} \] Чтобы обнаружить частицу в таком тонком слое (чтобы отличить её положение внутри запрещённой зоны от её положения вне этой зоны), нам необходимы кванты света с длиной волны \(\lambda < d\) или с частотой: \[ \nu = \frac{c}{\lambda} > \frac{c\sqrt{2m(U-E)}}{\hbar} \] Это неравенство можно переписать в эквивалентном виде: \[ (h\nu)^2 > 8\pi^2mc^2(U-E) \] Поскольку мы рассматриваем нерелятивистскую квантовую механику (в релятивистском случае уравнение Шрёдингера не применимо), то заведомо должно выполняться \(h\nu < mc^2\), поэтому поделив левую часть неравенства на меньшую величину \(h\nu\), а правую — на большую величину \(32\pi^2mc^2\), мы получим заведомо выполняющееся неравенство: \[ h\nu > U-E \] То есть для измерения положения частицы в запрещённой области необходимо подействовать на неё частицей (в данном случае фотоном), энергия которой больше разницы между потенциальной энергией и полной энергией измеряемой частицы в стационарном состоянии. Естественно, что в процессе такого взаимодействия измеряемая частица может получить достаточно энергии, чтобы её полная энергия стала больше потенциальной.
6.4 Потенциальный барьер и туннельный эффект
Возможность проникновения частицы в запрещённую область является одним из важнейших свойств квантовых систем, и в случае если запрещённая зона имеет конечную толщину, приводит к возможности так называемого туннелирования. Рассмотрим этот эффект подробнее.
Рассмотрим решение уравнения Шрёдингера в другом частном случае потенциальных функций — потенциальных барьеров. Потенциальным барьером будем называть всюду положительный одномерный потенциал, стремящийся к нулю на одной из бесконечностей и к некой константе (возможно, тоже нулю) на другой.
Для простоты рассмотрим случай прямоугольного потенциального барьера, с равными по величине потенциалами слева и справа от него. Пусть высота барьера \(U_0\), а координаты его границ — \(x=a, x=b, a < b\).
Разобьём пространство на три кусочно-однородные области: \[ I: x < a \] \[ II: a < x < b \] \[ III: x > b \] Потенциальная функция будет иметь вид: \[ U(x) = 0, x < a, x > b \] \[ U(x) = U_0, a < x < b \]
Запишем стационарное уравнение Шрёдингера в областях \(I\) и \(III\): \[ - \frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi = E\psi \] Введя \(k^2=\frac{2mE}{\hbar^2}\), перепишем его в виде \[ \frac{d^2}{dx^2}\psi + k^2\psi = 0 \] Линейно независимыми решениями этого уравнения являются функции \(e^{ikx}\) и \(e^{-ikx}\), составим из них решения в областях \(I\) и \(III\): \[ \psi_1 = A_1 e^{ikx} + B_1 e^{-ikx} \] \[ \psi_2 = A_3 e^{ikx} + B_3 e^{-ikx} \] Слагаемые в этих решениях имеют ясный физический смысл. Действительно, если мы рассмотрим полную волновую функцию \(\Psi = \psi(x)e^{i\omega t}\), то слагаемые с коэффициентами \(A_{1,3}\) отвечают волнам, бегущим вдоль оси \(x\), а слагаемые с коэффициентами \(B_{1,3}\) — волнам, бегущим против оси \(x\).
Если мы рассматриваем задачу о падении на барьер частицы, первоначально летящей вдоль оси \(x\), то волна \(A_1 e^{ikx}\) соответствует падающей частице, \(B_1 e^{—ikx}\) — отражённой частице, \(A_3 e^{ikx}\) — прошедшей частице и \(B_3 e^{-ikx}\) — отсутствующей в этом случае частицы, летящей изначально против оси \(x\). По последней причине мы должны положить \(B_3 = 0\).
Кроме того, мы должны наложить на решение условие нормировки, но в рассматриваемом нами идеализированном случае нормировочный интеграл расходится (функции \(\psi_{1,3}\) не стремятся на бесконечности к нулю), поэтому нормировка может быть произведена произвольным образом. Выберем её таким образом, чтобы \(A_1 = 1\), тогда квадраты модулей амплитуд \(B_1\) и \(A_3\) определят соответственно вероятности отражения и прохождения частицы при падении барьер.
В области \(II\) стационарное уравнение Шрёдингера будет иметь вид \[ - \frac{\hbar^2}{2m}\frac{d^2}{dx^2}\psi + U_0\psi = E\psi \] Рассмотрим наиболее интересный случай частицы, энергия которой меньше величины барьера: \(E < U_0\). Тогда введя \(\kappa^2=\frac{2m}{\hbar^2}(U_0 - E)\), получим: \[ \frac{d^2}{dx^2}\psi - \kappa^2\psi = 0 \] Решением этого уравнения будет функция \[ \psi_2 = A_2e^{\kappa x} + B_2e^{-\kappa x} \] Таким образом, мы имеем 4 неизвестные переменные. Чтобы их найти запишем условия непрерывности функции \(\psi\) и её производных в точках разрыва потенциальной функции: \[ \psi_1(a) = \psi_2(a) \] \[ \frac{d}{dx}\psi_1(a) = \frac{d}{dx}\psi_2(a) \] \[ \psi_2(b) = \psi_3(b) \] \[ \frac{d}{dx}\psi_2(b) = \frac{d}{dx}\psi_3(b) \] Получили систему четырёх линейных уравнений с четырьмя неизвестными. Решая её, находим нужные нам амплитуды: \[ B_1 = \frac{(\kappa^2 + k^2)(e^{\kappa d} - e^{-\kappa d})}{(\kappa + ik)^2e^{-\kappa d} - (\kappa - ik)^2e^{\kappa d}} \] \[ A_3 = \frac{4ik\kappa e^{-ikd}}{(\kappa + ik)^2e^{-\kappa d} - (\kappa - ik)^2e^{\kappa d}} \] где \(d = b - a\). Отметим, что \[ |B_1|^2 + |A_3|^2 = 1 \] Квадраты модулей амплитуд \(|B_1|^2\) и \(|A_3|^2\) следует интерпретировать как вероятности обнаружения отражённой или прошедшей частицы соответственно.
Отличие вероятности \(|A_3|^2\) от нуля является чисто квантовым эффектом. В классической физике частица с энергией, меньшей величины барьера, всегда отражается. Этот эффект носит название туннельного эффекта и играет фундаментальную роль во многих процессах микромира.
В заключение отметим, что решение для прямоугольного барьера можно обобщить на случай произвольного достаточно плавного барьера. Для этого вычислим коэффициент прохождения в приближении \(\kappa d \gg 1\): \[ D = |A_3|^2 \approx \frac{16k^2\kappa^2}{(k^2+\kappa^2)}e^{-2\kappa d} \] Если разбить произвольный потенциал на множество прямоугольных потенциалов толщины \(dx\) и считать потенциал достаточно плавным, так что можно удовлетворить условию \(\kappa dx \gg 1\), то коэффициенты прохождения последовательно расположенных прямоугольных потенциалов будут перемножаться, поэтому полный коэффициент прохождения будет равен: \[ D \sim \exp{\left\{-\frac{2}{\hbar}\int\sqrt{2m(U(x) - E)}dx\right\}} \] где интегрирование ведётся по области локализации потенциального барьера.
Туннельный эффект имеет целый ряд важных практических применений. Рассмотрим некоторые из них.
Автоэлектронная эмиссия — это процесс испускания электронов поверхностью проводящих тел при наличии внешнего электрического поля, перпендикулярного поверхности. Это явление было впервые обнаружено ещё в 1897 году Р. Вудом, но адекватная теоретическая модель, объясняющая его через квантовое туннелирование, появилась только в 1928–1929 годах в работах Р. Фаулера и Л. Нордхейма.
В известном смысле эффект аналогичный автоэлектронной эмиссии наблюдается и в атомах, помещённых в сильное переменное поле лазерного излучения. При этом наблюдается так называемая туннельная ионизация.
Альфа-распад атомных ядер, открытый ещё Антуаном Анри Беккерелем, также может быть объяснён как квантовое туннелирование альфа-частицы (ядра гелия-4, то есть системы из двух протонов и двух нейтронов) из ядра. Такая теория была впервые построена Г. Гамовым в 1927 году.
Наконец, туннельный эффект используется в туннельных микроскопах, с помощью которых удаётся строить рельеф поверхности проводящих тел с точностью до одного ангстрема вдоль поверхности и сотых долей ангстрема по высоте.
6.5 Постулаты квантовой механики и операторы физических величин
До сих пор, рассматривая описание состояний частиц волновыми функциями, мы интересовались только положением этих частиц в пространстве — то есть функцией распределения вероятности их обнаружения в той или иной точке. Однако при решении задач зачастую необходимо знать не только координаты частицы, но и другие её характеристики — импульс, момент импульса, энергию и т. п. Возникает вопрос, как их определить (хотя бы с точностью до соответствующей плотности вероятности), если известна волновая функция частицы.
На этот вопрос отвечают постулаты квантовой механики. Перечислим их:
- Состояние квантовой системы описывается функцией \(\Psi(q_1, \dots, q_n, t)\), зависящей от обобщённых координат всех частиц, входящих в рассматриваемую систему, и от времени. Эта функция носит название функции состояния или волновой функции системы.
- Каждой динамической переменной (координате, импульсу, моменту импульса, энергии и т. п.) ставится в соответствие некий вполне определённый линейный самосопряжённый оператор, вид которого постулируется. Напомним, что линейность оператора \(\hat A\) означает выполнение для любых функций состояния \(\Psi\) и \(\Phi\) и любых комплексных констант \(\alpha\) и \(\beta\): \[ \hat A(\alpha\Psi + \beta\Phi) = \alpha\hat A\Psi + \beta\hat A\Phi \] Самосопряжённость оператора означает, что выполняется: \[ \int\Psi^*\hat A\Psi dq = \int\Psi \hat A^*\Psi^* dq \] При этом функциональные соотношения между переменными, имевшие место в классической механике, заменяются на аналогичные соотношения между операторами. Например, соотношение между кинетической энергий и импульсом: \[ T = \frac{1}{2m}p^2 \] заменяется на аналогичное соотношение между соответствующими операторами: \[ \hat T = \frac{1}{2m} \hat{p^2} \]
- Функция состояния подчиняется уравнению Шрёдингера вида \[ i\hbar\frac{\partial}{\partial t}\Psi = \hat H\Psi \] где \(\hat H\) — оператор Гамильтона, соответствующий функции Гамильтона (гамильтониану) классической механики.
- При измерении значения динамической переменной \(A\) оно может принимать только те значения, которые являются собственными для уравнения: \[ \hat A\Psi = A\Psi \]
- При проведении большого количества измерений систем в одном и том же состоянии \(\Psi\) среднее значение физической величины определяется выражением: \[ \langle A \rangle = \int \Psi^* \hat A \Psi dq \equiv \langle \Psi | A | \Psi \rangle \] Из этого постулата можно вывести также и вероятности получения того или иного значения в случае дискретного набора собственных значений оператора. Действительно, пусть \(A_i, \Psi_i\) — собственные значения и функции оператора \(\hat A\), т. е. выполняется: \[ \hat A\Psi_i = A_i\Psi_i \] Тогда из общей теории операторов известно, что функции \(\Psi_i\) образуют полный ортонормированный базис, то есть любая функция состояния \(\Psi\) может быть представлена в виде: \[ \Psi = \sum c_i\Psi_i \] Распишем выражение для среднего через коэффициенты \(c_i\): \[ \langle A \rangle = \langle \Psi | A | \Psi \rangle = \left\langle \sum\limits_i c_i^*\Psi_i | A | \sum\limits_j c_j\Psi_j \right\rangle = \] \[ = \sum\limits_i\sum\limits_j c_i^*c_j \langle \Psi_i | A | \Psi_j \rangle = \sum\limits_i\sum\limits_j c_i^*c_j A_j \langle \Psi_i | \Psi_j \rangle \] В силу ортонормированности базиса: \[ \langle \Psi_i | \Psi_j \rangle = \delta_{ij} \] где \(\delta_{ij}\) — символ Кронекера, равный 1, если \(i=j\), и 0 если \(i\neq j\). Окончательно получаем: \[ \langle A \rangle = \sum\limits_i |c_i|^2 A_i \] Отсюда видно, что величина \(|c_i|^2\) имеет смысл вероятности получить при измерении значение \(A_i\). Найти коэффициенты \(c_i\), зная функцию \(\Psi\), можно, взяв следующий интеграл: \[ c_i = \int \Psi_i^*\Psi dq \equiv \langle \Psi_i | \Psi \rangle \] Действительно: \[ \int \Psi_i^*\Psi dq = \int \Psi_i^* \sum\limits_j c_j\Psi_j dq = \sum\limits_j c_j \int \Psi_i^* \Psi_j dq = \sum\limits_j c_j \delta_{ij} = c_i \]
- Если система может находиться в состояниях, описываемых функциями \(\Psi_1\) и \(\Psi_2\), то она может находиться и в состоянии \(\Psi = c_1\Psi_1 + c_2\Psi_2\) (свойство линейности). Коэффициенты \(c_{1,2}\) можно найти, взяв интегралы: \[ c_{1,2} = \int \Psi^*\Psi_{1,2}dq \] Кроме того, величины \(|c_{1,2}|^2\) равны вероятности обнаружения системы в состоянии \(\Psi_i\).
6.6 Операторы
Оператором называется правило, по которому функции из одного множества ставится в соответствие функция из другого множества: \[ \hat A: \Psi(q) \rightarrow \Phi(q) \] Частными случаями операторов являются:
- Оператор умножения на некое комплексное число \(\lambda\): \[ \Psi(q) \rightarrow \Phi(q) = \lambda \Psi(q) \]
- Оператор умножения на некую функцию от обобщённых координат: \[ \Psi(q) \rightarrow \Phi(q) = f(q) \Psi(q) \]
- Оператор взятия частной производной по одной из обобщённых координат: \[ \Psi(q) \rightarrow \Phi(q) = \frac{\partial}{\partial q_i} \Psi(q) \]
- Произвольные комбинации вышеприведённых операторов
Над операторами можно осуществлять некоторые операции. Например, сложение: \(\hat B = \hat A_1 + \hat A_2\). Суммой операторов \(\hat A_1, \hat A_2\) называется оператор \(\hat B\), результат действия которого на произвольную функцию \(\Psi\) равен сумме \(\hat B\Psi = \hat A_1\Psi + \hat A_2\Psi\).
Можно ввести также и произведение операторов \(\hat B = \hat A_1 \hat A_2\). Произведением операторов \(\hat A_1, \hat A_2\) называется оператор \(\hat B\), результат действия которого на произвольную функцию \(\Psi\) равен последовательному действию на неё перемножаемых операторов \(\hat B\Psi = \hat A_1 \left( \hat A_2\Psi \right)\).
Из операций сложения и умножения можно составить произвольную целую рациональную функцию \(\hat L(\hat A_1, \hat A_2)\), которая также будет оператором.
6.6.1 Коммутативность операторов и одновременная измеримость
В отличие от обычной алгебры произведение операторов в общем случае некоммутативно, то есть: \[ \hat A_1 \hat A_2 \neq \hat A_2 \hat A_1 \] Примером могут служить операторы умножения на функцию \(f(x) = x\) и взятие производной \(\frac{\partial}{\partial x}\). Действительно: \[ \hat A_1 \hat A_2 \Psi = \left(x\frac{\partial}{\partial x}\right)\Psi = x\frac{\partial\Psi}{\partial x} \] \[ \hat A_2 \hat A_1 \Psi = \left(\frac{\partial}{\partial x}x\right)\Psi = \Psi + x\frac{\partial\Psi}{\partial x} \] Величина \(\hat A_1 \hat A_2 - \hat A_2 \hat A_1\) называется коммутатором. В данном примере он равен 1. Если коммутатор равен нулю, то говорят, что операторы коммутируют.
Оказывается, что свойство коммутативности операторов в квантовой механике связано с возможностью одновременной измеримости соответствующих им физических величин. Напомню, что согласно принципу неопределённости Гейзенберга, не все физические величины могут быть измерены одновременно со сколь угодно высокой точностью. В частности, чем точнее мы измеряем координату частицы \(x\), тем меньше точность нашего знания о её импульсе \(p_x\), и наоборот.
Чтобы две величины \(A\) и \(B\) были измеримы одновременно, необходимо, чтобы существовали такие состояния, в которых обе эти величины имели определённое значение. Физическая величина имеет определённое значение в состоянии, описываемом собственной функцией соответствующего оператора. Таким образом, чтобы величины \(A\) и \(B\) были одновременно измеримы, необходимо, чтобы соответствующие им операторы \(\hat A\) и \(\hat B\) имели совпадающие собственные функции: \[ \hat A \psi_n = A_n \psi_n \] \[ \hat B \psi_n = B_n \psi_n \] Применим к первому из этих равенств оператор \(\hat B\): \[ \hat B\hat A \psi_n = \hat B A_n \psi_n = A_n \hat B \psi_n = A_n B_n \psi_n \] Аналогично, применяя ко второму равенству оператор \(\hat A\), получаем: \[ \hat A\hat B \psi_n = \hat A B_n \psi_n = B_n \hat A \psi_n = B_n A_n \psi_n \] Сравнивая правые части равенств, приходим к выводу, что \[ (\hat B \hat A - \hat A \hat B) \psi_n = \hat B \hat A \psi_n - \hat A \hat B \psi_n = 0 \] Поскольку мы по условию предположили, что величины одновременно измеримы всегда, а не только в отдельных состояниях, то из этого равенства следует и равенство нулю самого коммутатора: \[ \hat B \hat A - \hat A \hat B = 0 \] Таким образом, если две физические величины одновременно измеримы, то соответствующие им операторы коммутируют.
Можно доказать и обратное утверждение: если операторы двух физических величин коммутируют, то они одновременно измеримы.
Эти два утверждения можно объединить в одно:
Две физические величины одновременно измеримы, вообще говоря, тогда и только тогда, когда соответствующие им операторы коммутируют.
6.6.2 Операторы основных физических величин
6.6.2.1 Оператор координаты
Оператор координаты частицы \(\hat x\) представляет собой простое умножение на соответствующую координату \(x\): \[ \hat x \psi = x \psi \] Действительно, рассмотрим среднее значение этого оператора: \[ <x> = \int \psi^* \hat x \psi dx = \int \psi^* x \psi dx = \int x |\psi|^2 dx \] Поскольку величина \(|\psi|^2dx\) имеет смысл вероятности обнаружения частицы в интервале \(dx\), то справа как раз стоит среднее значение координаты \(x\).
Согласно свойствам операторов, оператор любой функции от координат представляет собой умножение на соответствующую функцию: \[ \hat U(\hat{\vec r})\psi = U(\vec r)\psi \]
6.6.2.2 Оператор импульса
Оператор проекции импульса частицы \(\hat p_x\) имеет следующий вид: \[ \hat p_x = -i\hbar\frac{\partial}{\partial x} \] Можно ввести и оператор вектора импульса: \[ \hat{\vec p} = \vec x_0 \hat p_x + \vec y_0 \hat p_y + \vec z_0 \hat p_z = -i\hbar \left(\vec x_0 \frac{\partial}{\partial x} + \vec y_0 \frac{\partial}{\partial y} + \vec z_0 \frac{\partial}{\partial z}\right) \equiv -i\hbar\nabla \]
Найдём собственные функции оператора импульса: \[ \hat p_x \psi = p_x \psi \] \[ -i\hbar\frac{\partial \psi}{\partial x} = p_x \psi \] \[ \psi(x) = A\exp\left(i\frac{p_x}{\hbar}x\right) \] Несложно видеть, что частным случаем собственной функции оператора импульса являются волны де Бройля, пространственная часть которых удовлетворяет этому уравнению. Это и неудивительно, поскольку волны де Бройля вводились как функции состояния частиц с определённым импульсом.
Зная операторы координаты и импульса, можно теперь находить операторы и других величин, являющихся простыми целыми функциями координат и импульса. Если для некой величины \(A\) справедливо \(A = F(\vec r, \vec p)\), то оператор этой величины \(\hat A = \hat F\left(\hat {\vec r}, \hat {\vec p}\right)\). Ниже рассматриваются примеры таких величин.
6.6.2.3 Оператор полной энергии
Для частицы, движущейся в поле потенциальных сил, полная энергия может быть записана в виде: \[ H = \frac{p^2}{2m} + U(\vec r) \] Это выражение совпадает с функцией Гамильтона этой частицы. Соответствующий ей оператор носит название оператора Гамильтона или гамильтониана: \[ \hat H = \frac{\hat{p^2}}{2m} + \hat U (\hat {\vec r}) \] Распишем операторы справа: \[ \hat H = \frac{1}{2m}(-i\hbar\nabla)^2 + U(\vec r) = -\frac{\hbar^2}{2m}\Delta + U(\vec r) \] С таким выражением мы уже сталкивались при записи уравнения Шрёдингера, таким образом, оно может быть записано в символическом виде \[ i\hbar\frac{\partial\psi}{\partial t} = \hat H\psi \] Если понимать здесь под \(\hat H\) функцию Гамильтона, то уравнение в таком виде справедливо и для частиц в магнитном поле (в этом случае гамильтониан системы не совпадает с выражением для полной энергии). В случае же только потенциальных сил оператор Гамильтона и оператор полной энергии совпадают, и поэтому уравнение на поиск собственных функций оператора Гамильтона представляет собой стационарное уравнение Шрёдингера: \[ \hat H \psi = E \psi \] Это уравнение одновременно позволяет находить и собственные функции и собственные значения оператора полной энергии.
6.6.2.4 Оператор момента импульса
В классической физике момент импульса определяется формулой: \[ \vec L = \left[ \vec r \times \vec p \right] \] Поэтому формально оператор вектора момента импульса можно записать как: \[ \hat {\vec L} = \left[ \hat {\vec r} \times \hat {\vec p} \right] \] Распишем его в проекциях: \[ \hat L_x = \left(\hat y \hat p_z - \hat z \hat p_y\right) = i\hbar\left(z\frac{\partial}{\partial y} - y\frac{\partial}{\partial z}\right) \] \[ \hat L_y = \left(\hat z \hat p_x - \hat x \hat p_z\right) = i\hbar\left(x\frac{\partial}{\partial z} - z\frac{\partial}{\partial x}\right) \] \[ \hat L_z = \left(\hat x \hat p_y - \hat y \hat p_x\right) = i\hbar\left(y\frac{\partial}{\partial x} - x\frac{\partial}{\partial y}\right) \] Зададимся теперь вопросом: измеримы ли одновременно разные проекции момента импульса? Для ответа на него найдём коммутатор операторов двух произвольных проекций, например, \(\hat L_x\) и \(\hat L_y\). Вычислим сначала \(\hat L_x \hat L_y\): \[ \hat L_x \hat L_y \psi = i\hbar\left(z\frac{\partial}{\partial y} - y\frac{\partial}{\partial z}\right)i\hbar\left(x\frac{\partial}{\partial z} - z\frac{\partial}{\partial x}\right)\psi = \] \[ =-\hbar^2\left(z\frac{\partial}{\partial y} - y\frac{\partial}{\partial z}\right)\left(x\frac{\partial\psi}{\partial z} - z\frac{\partial\psi}{\partial x}\right) = \] \[ =-\hbar^2\left(zx\frac{\partial^2\psi}{\partial y \partial z} - yx\frac{\partial^2\psi}{\partial z^2} - z^2\frac{\partial^2\psi}{\partial y \partial x} + yz\frac{\partial^2\psi}{\partial z \partial x} + y\frac{\partial\psi}{\partial x}\right) \] Для обратного порядка \(\hat L_y \hat L_x\) аналогично имеем: \[ \hat L_y \hat L_x \psi = i\hbar\left(x\frac{\partial}{\partial z} - z\frac{\partial}{\partial x}\right)i\hbar\left(z\frac{\partial}{\partial y} - y\frac{\partial}{\partial z}\right)\psi = \] \[ =-\hbar^2\left(x\frac{\partial}{\partial z} - z\frac{\partial}{\partial x}\right)\left(z\frac{\partial\psi}{\partial y} - y\frac{\partial\psi}{\partial z}\right) = \] \[ =-\hbar^2\left(zy\frac{\partial^2\psi}{\partial x \partial z} - xy\frac{\partial^2\psi}{\partial z^2} - z^2\frac{\partial^2\psi}{\partial x \partial y} + xz\frac{\partial^2\psi}{\partial z \partial y} + x\frac{\partial\psi}{\partial y}\right) \] Вычитая \(\hat L_x \hat L_y - \hat L_y \hat L_x\), видим, что большинство членов сокращается и остаётся только: \[ \hat L_x \hat L_y - \hat L_y \hat L_x = -\hbar^2\left(y\frac{\partial}{\partial x} - x\frac{\partial}{\partial y}\right) = i\hbar \hat L_z \] Таким образом, операторы проекций момента импульса взаимно не коммутируют, и следовательно, проекции момента импульса на разные оси одновременно неизмеримы.
6.6.2.5 Оператор квадрата модуля полного момента импульса
Мы можем, однако, рассмотреть ещё одну величину — модуль момент импульса или, что эквивалентно, квадрат модуля момента импульса: \[ L^2 = L_x^2 + L_y^2 + L_z^2 \] Оператор этой величины имеет вид: \[ \hat{L^2} = \hat L_x^2 + \hat L_y^2 + \hat L_z^2 \] Определим его коммутационные свойства с оператором одной из проекций: \[ \hat{L^2}\hat L_z = (\hat L_x^2 + \hat L_y^2 + \hat L_z^2)\hat L_z = \] \[ =\hat L_x (\hat L_x \hat L_z) + \hat L_y (\hat L_y \hat L_z) + \hat L_z^3 = \] \[ =\hat L_x (\hat L_z \hat L_x - i\hbar \hat L_y) + \hat L_y (\hat L_z \hat L_y + i\hbar \hat L_x) + \hat L_z^3 \] Аналогично: \[ \hat L_z\hat{L^2} = \hat L_z(\hat L_x^2 + \hat L_y^2 + \hat L_z^2) = \] \[ =(\hat L_z \hat L_x)\hat L_x + (\hat L_z \hat L_y)\hat L_y + \hat L_z^3 = \] \[ =(\hat L_x \hat L_z + i\hbar \hat L_y)\hat L_x + (\hat L_y \hat L_z - i\hbar \hat L_x)\hat L_y + \hat L_z^3 \] Сравнивая получившиеся выражения, видим, что они полностью совпадают, то есть: \[ \hat{L^2}\hat L_z - \hat L_z\hat{L^2} = 0 \] Таким образом, оператор квадрата модуля момента импульса коммутирует с операторами проекции момента импульса, и следовательно, они одновременно измеримы. Другими словами, существуют такие состояния частицы, в которых квадрат модуля и одна из проекций момента импульса имеют определённые значения.
6.7 Квантование момента импульса
6.7.1 Собственные значения и собственные функции оператора проекции момента импульса
В силу особой значимости момента импульса для анализа задачи о квантовании атома рассмотрим свойства операторов проекции и квадрата модуля момента импульса подробнее. В частности, найдём их собственные значения.
Согласно постулатам квантовой механики для этого нам необходимо решить уравнения вида \[ \hat L_z \Psi = L_z \Psi \] \[ \hat {L^2} \Psi = L^2 \Psi \] Удобно рассмотреть их в сферической системе координат, которую введём следующим образом: \[ x = r\sin\vartheta\cos\phi \] \[ y = r\sin\vartheta\sin\phi \] \[ z = r\cos\vartheta \] В этой системе координат операторы проекций момента импульса запишутся в виде: \[ \hat L_x = i\hbar\left(\sin\phi\frac{\partial}{\partial\vartheta} + \rm{ctg}\vartheta\cos\phi\frac{\partial}{\partial\phi}\right) \] \[ \hat L_y = i\hbar\left(-\cos\phi\frac{\partial}{\partial\vartheta} + \rm{ctg}\vartheta\sin\phi\frac{\partial}{\partial\phi}\right) \] \[ \hat L_z = -i\hbar\frac{\partial}{\partial\phi} \] Как видим, эти операторы не зависят от радиальной координаты, то есть определяют зависимость волновой функции только от угловых переменных.
Для собственных значений оператора \(\hat L_z\) имеем следующее уравнение: \[ \hat L_z\Psi = L_z\Psi \] \[ -i\hbar\frac{\partial\Psi}{\partial \phi} = L_z\Psi \] Его решением являются функции вида \[ \Psi = C(r,\vartheta)\exp\left({i\frac{L_z}{\hbar}\phi}\right) \] Поскольку функция \(\Psi\) по своему физическому смыслу должна быть однозначной функцией координат, то должно выполняться условие: \[ \Psi(\phi) = \Psi(\phi+2\pi) \] \[ \exp\left({i\frac{L_z}{\hbar}\phi}\right) = \exp\left({i\frac{L_z}{\hbar}(\phi+2\pi)}\right) \] \[ \exp\left({i\frac{L_z}{\hbar}2\pi}\right) = 1 \] \[ \frac{L_z}{\hbar}2\pi = 2\pi m \] \[ L_z = \hbar m \] где \(m\) может принимать значения \(0, \pm 1, \pm 2,\dots\)
Число \(m\) определяет величину проекции момента импульса на ось \(z\) и носит название магнитного квантового числа.
6.7.2 Собственные значения оператора квадрата момента импульса
Формально для поиска собственных значений оператора квадрата момента импульса \(\hat{L^2}\) необходимо исследовать уравнение \[ \hat {L^2}\Psi = L^2\Psi \] и найти такие значения \(L^2\), при которых оно имеет решения, имеющие физический смысл.
Однако собственные значения оператора \(\hat{L^2}\) можно найти и исходя из чисто операторных соотношений. Этот путь мы здесь и рассмотрим.
Для начала докажем, что если система находится в состоянии с определёнными квадратом и проекцией момента импульса, то \(L^2 > L_z^2 = \hbar^2m^2\). Действительно, поскольку операторы \(\hat{L^2}\) и \(\hat L_z\) коммутируют, то соответствующие им физические величины одновременно измеримы, и поэтому существует такой полный набор состояний \(\Psi\), в каждом из которых \(L^2\) и \(L_z\) имеют определённое значение. Рассмотрим одно из таких состояний и найдем в этом состоянии среднее значение величины \(A = L^2 - L_z^2 = L_x^2 + L_y^2\): \[ \langle A \rangle = \langle \Psi | \hat A| \Psi \rangle = \langle \Psi | \hat {L^2} - \hat L_z^2| \Psi \rangle = \langle \Psi | \hat L_x^2 + \hat L_y^2| \Psi \rangle \] Поскольку величины \(L_x^2\) и \(L_y^2\) существенно неотрицательны, то и среднее от их суммы тоже неотрицательная величина, поэтому: \[ \langle L^2 - L_z^2 \rangle \ge 0 \] С другой стороны, поскольку мы рассматриваем состояние, в котором \(L^2\) и \(L_z\) имеют определённое значение, то их средние просто совпадают с их значениями, поэтому: \[ \langle L^2 - L_z^2 \rangle = L^2 - L_z^2 \ge 0 \] Откуда: \[ L^2 \ge L_z^2 = \hbar^2m^2 \]
Введём следующие вспомогательные операторы: \[ \hat L_+ = \hat L_x + i \hat L_y \] \[ \hat L_- = \hat L_x - i \hat L_y \] Найдём коммутаторы этих операторов между собой и с оператором \(\hat L_z\): \[ \hat L_+\hat L_- - \hat L_-\hat L_+ = (\hat L_x + i \hat L_y)(\hat L_x - i \hat L_y) - (\hat L_x - i \hat L_y)(\hat L_x + i \hat L_y) = \] \[ = -2i(\hat L_x\hat L_y - i \hat L_y \hat L_x) = 2\hbar\hat L_z \] \[ \hat L_z\hat L_+ - \hat L_+\hat L_z = \hat L_z(\hat L_x + i \hat L_y) - (\hat L_x + i \hat L_y)\hat L_z = \] \[ = (\hat L_z\hat L_x - \hat L_x\hat L_z) + i(\hat L_z\hat L_y - \hat L_y \hat L_z) = i\hbar\hat L_y + \hbar\hat L_x = \hbar\hat L_+ \] \[ \hat L_z\hat L_- - \hat L_-\hat L_z = \hat L_z(\hat L_x - i \hat L_y) - (\hat L_x - i \hat L_y)\hat L_z = \] \[ = \hat L_z\hat L_- - \hat L_-\hat L_z = \hat L_z(\hat L_x - i \hat L_y) - (\hat L_x - i \hat L_y)\hat L_z = i\hbar\hat L_y - \hbar\hat L_x = -\hbar\hat L_- \] Далее представим оператор \(\hat {L^2}\) в следующем виде: \[ \hat{L^2} = \hat L_x^2 + \hat L_y^2 + \hat L_z^2 = \left(\frac{\hat L_+ + \hat L_-}{2}\right)^2 + \left(\frac{\hat L_+ - \hat L_-}{2i}\right)^2 + \hat L_z = \] \[ =\frac{1}{4}(\hat L_+\hat L_- + \hat L_-\hat L_+) + \frac{1}{4}(\hat L_+\hat L_- + \hat L_-\hat L_+) + \hat L_z^2 = \] \[ = \frac{1}{2}(\hat L_+\hat L_- + \hat L_-\hat L_+) + \hat L_z^2 = \hat L_+\hat L_- + \hat L_z^2 - \hbar\hat L_z = \hat L_-\hat L_+ + \hat L_z^2 + \hbar\hat L_z \] Рассмотрим теперь только такие состояния, в которых \(L^2\) имеет некую фиксированную величину, тогда в таких состояниях \(m < \frac{L}{\hbar}\). Выберем из этих состояний такое состояние \(\Psi\), в котором \(m\) принимает наибольшее значение, и обозначим его за \(l\): \[ \hat L_z\Psi = \hbar l\Psi \] Рассмотрим действие на это состояние операторов \(\hat L_z\hat L_\pm\): \[ \hat L_z\hat L_\pm\Psi = (\hat L_\pm\hat L_z\pm\hbar\hat L_\pm)\Psi = \hbar (l\pm 1)\hat L_\pm\Psi \] Отсюда видно, что функции \(\Phi_\pm = \hat L_\pm\Psi\) являются собственными функциями оператора \(\hat L_z\) с собственными значениями \(\hbar(l\pm 1)\). Однако по выбранному нами условию \(\hbar l\) является максимальным собственным значением оператора \(\hat L_z\), поэтому функция \(\Phi_+\) не может быть собственной функцией этого оператора. Противоречие можно разрешить, только если предположить, что \(\Phi_+ \equiv 0\) (нулевое решение удовлетворяет уравнению на собственные функции и значения, но не имеет определённого собственного значения). Получаем: \[ \hat L_+\Psi = 0 \] Подействуем на это уравнение оператором \(\hat L_-\): \[ \hat L_-\hat L_+\Psi = 0 \] \[ (\hat {L^2} - \hat L_z^2 - \hbar\hat L_z)\Psi = 0 \] \[ \hat {L^2}\Psi - \hbar^2l^2\Psi - \hbar^2l\Psi = 0 \] \[ \hat {L^2}\Psi = \hbar^2(l+1)l\Psi \] Откуда видим, что собственное значение оператора \(\hat {L^2}\) равно \(L^2 = \hbar^2(l+1)l\).
Число \(l\) называют орбитальным квантовым числом.
Зададимся вопросом, сколько существует линейно независимых состояний, в которых \(L^2 = \hbar^2(l+1)l\). По условию \(m \le l\), поэтому число \(m\) может принимать значения \(-l,\dots,0,\dots,l\). Таких значений — \(2l+1\), то есть существует \(2l+1\) состояние с заданным числом \(l\) и различными числами \(m\).
6.7.3 Сложение моментов импульса частиц
Рассмотрим систему частиц, каждая из которых имеет некий момент импульса. Рассмотрим вопрос о свойствах их суммарного момента импульса. Для простоты рассмотрим систему из двух частиц.
В общем случае не существует простой связи между правилами квантования суммарного момента импульса системы частиц и моментов импульса каждой из частиц. Однако такие правила можно получить в случае, если можно пренебречь взаимодействием между частицами.
Состояние системы двух частиц в общем случае должно описываться функцией, зависящей от обобщённых координат каждой из частиц \(\Psi (q_1, q_2)\), однако для невзаимодействующих частиц эта функция может быть факторизована: \[ \Psi (q_1, q_2) = \Psi_1(q_1)\Psi_2(q_2) \] В этом случае можно показать, что операторы проекций момента импульса, относящиеся к разным частицам, коммутируют между собой. Например, для \(\hat L_{1x}\) и \(\hat L_{2y}\) \[ \hat L_{1x}\hat L_{2y} \Psi(q_1, q_2) = \hat L_{1x}\hat L_{2y}\left(\Psi_1(q_1)\Psi_2(q_2)\right) = \left(\hat L_{1x}\Psi_1\right)\left(\hat L_{2y}\Psi_2\right) = \] \[ = \left(\hat L_{2y}\Psi_2\right)\left(\hat L_{1x}\Psi_1\right) = \hat L_{2y}\hat L_{1x} \Psi(q_1, q_2) \] Точно так же можно показать, что коммутируют между собой и операторы квадрата момента импульса \(\hat{L_1^2}\) и \(\hat{L_2^2}\), а также операторы \(\hat{L_1^2}\) и \(\hat L_{2x}\) и т. д.
Покажем теперь, что коммутируют между собой операторы квадрата и проекции момента импульса системы частиц \(\hat{L^2}\) и \(\hat L_{z}\).
Поскольку в классической физике выполняются соотношения \[ \vec L = \vec L_1 + \vec L_2 \] \[ L_z = L_{1z} + L_{2z} \] \[ L^2 = L_1^2 + L_2^2 + 2\left(\vec L_1\cdot\vec L_2\right) \] то в квантовой физике аналогичные соотношения выполняются для соответствующих операторов: \[ \hat L_z = \hat L_{1z} + \hat L_{2z} \] \[ \hat {L^2} = \hat{L_1^2} + \hat{L_2^2} + 2\left(\hat{\vec{L_1}}\cdot\hat{\vec{L_2}}\right) \] Поскольку операторы \(\hat L_{1z}\), \(\hat L_{2z}\), \(\hat{L_1^2}\), \(\hat{L_2^2}\) попарно коммутируют, то надо доказать только, что коммутируют \(\hat L_z\) и \(\left(\hat{\vec{L_1}}\cdot\hat{\vec{L_2}}\right)\). Рассмотрим их коммутатор: \[ \left(\hat{\vec{L_1}}\cdot\hat{\vec{L_2}}\right)\hat L_z - \hat L_z\left(\hat{\vec{L_1}}\cdot\hat{\vec{L_2}}\right) = \] \[ = \left(\hat L_{1x}\hat L_{2x} + \hat L_{1y}\hat L_{2y} + \hat L_{1z}\hat L_{2z}\right)(\hat L_{1z} + \hat L_{2z}) - \] \[ - (\hat L_{1z} + \hat L_{2z})\left(\hat L_{1x}\hat L_{2x} + \hat L_{1y}\hat L_{2y} + \hat L_{1z}\hat L_{2z}\right) = \] \[ = (\hat L_{1x}\hat L_{2x}\hat L_{1z} - \hat L_{1z}\hat L_{1x}\hat L_{2x}) + (\hat L_{1y}\hat L_{2y}\hat L_{1z} - \hat L_{1z}\hat L_{1y}\hat L_{2y}) + \] \[ + (\hat L_{1z}\hat L_{2z}\hat L_{1z} - \hat L_{1z}\hat L_{1z}\hat L_{2z}) + (\hat L_{1x}\hat L_{2x}\hat L_{2z} - \hat L_{2z}\hat L_{1x}\hat L_{2x}) + \] \[ + (\hat L_{1y}\hat L_{2y}\hat L_{2z} - \hat L_{2z}\hat L_{1y}\hat L_{2y}) + (\hat L_{1z}\hat L_{2z}\hat L_{2z} - \hat L_{2z}\hat L_{1z}\hat L_{2z}) = \] \[ = (\hat L_{1x}\hat L_{1z} - \hat L_{1z}\hat L_{1x})\hat L_{2x} + (\hat L_{1y}\hat L_{1z} - \hat L_{1z}\hat L_{1y})\hat L_{2y} + \] \[ + (\hat L_{2x}\hat L_{2z} - \hat L_{2z}\hat L_{2x})\hat L_{1x} + (\hat L_{2y}\hat L_{2z} - \hat L_{2z}\hat L_{2y})\hat L_{1y} = \] \[ = -i\hbar\hat L_{1y}\hat L_{2x} + i\hbar\hat L_{1x}\hat L_{2y} -i\hbar\hat L_{2y}\hat L_{1x} + i\hbar\hat L_{2x}\hat L_{1y} = 0 \] Таким образом, операторы \(\hat{L^2}\) и \(\hat L_{z}\) коммутируют между собой, то есть правила квантования момента импульса системы невзаимодействующих систем совпадает с правилами квантования момента импульса одной частицы.
Представляет, однако, интерес найти связь между квантовыми числами частиц и их системы. Поскольку все операторы \(\hat L_{1z}\), \(\hat L_{2z}\), \(\hat{L_1^2}\), \(\hat{L_2^2}\) попарно коммутируют, то существует состояние \(\Phi_{l_1,m_1,l_2,m_2}\), в котором они имеют определённые собственные значения, характеризуемые квантовыми числами \(l_1,m_1,l_2,m_2\). При фиксированных \(l_1, l_2\) число таких состояний равно \((2l_1+1)(2l_2+1)\). Естественно, что путём линейной комбинации этих состояний можно получить любое состояние системы с заданными \(l_1\) и \(l_2\).
В то же время в силу равенства нулю попарных коммутаторов операторов \(\hat {L^2}\), \(\hat L_z\), \(\hat L_{1z}\), \(\hat L_{2z}\) среди этих состояний должны быть такие, в которых определены и собственные значения операторов \(\hat {L^2}\), \(\hat L_z\), характеризуемые числами \(l, m\), то есть тот же набор состояний может быть представлен в виде линейной комбинации некоторых функций \(\Psi_{l_1,l_2,l,m}\), число которых также должно быть равно \((2l_1+1)(2l_2+2)\). Это позволяет найти связь между числами \(l, m\) и \(l_1,m_1,l_2,m_2\).
Поскольку \(\hat L_z = \hat L_{1z} + \hat L_{2z}\), то: \[ \hat L_z\Psi_{l_1,l_2,l,m} = (\hat L_{1z} + \hat L_{2z})\Psi_{l_1,l_2,l,m} = (\hat L_{1z} + \hat L_{2z})\Phi_{l_1,m_1,l_2,m_2} = \] \[ = \hbar m_1\Phi_{l_1,m_1,l_2,m_2} + \hbar m_2\Phi_{l_1,m_1,l_2,m_2} = \hbar(m_1+m_2)\Phi_{l_1,m_1,l_2,m_2} = \] \[ = \hbar(m_1+m_2)\Psi_{l_1,l_2,l,m} \] То есть \(m = m_1 + m_2\).
Поскольку \(l, l_1, l_2\) — это максимальные значения, которые могут принимать числа \(m, m_1, m_2\), то из соотношения \(m = m_1 + m_2\) следует, что \(l \le l_1+l_2\), то есть \(l\) может принимать значения \(l = l_1+l_2, l_1+l_2-1, \dots\), и при каждом значении \(l\) существует \(2l+1\) состояния с различным \(m\). Подсчитаем их число, предположив, что минимальное значение \(l\) это \(l_1+l_2-n\): \[ \sum\limits_{l=l_1+l_2-n}^{l_1+l_2}(2l+1) \] Это арифметическая прогрессия из \(n+1\) члена с шагом \(2\), её сумма: \[ \sum\limits_{l=l_1+l_2-n}^{l_1+l_2}(2l+1) = \frac{n+1}{2}\Big[2(l_1+l_2-n)+1 + 2(l_1+l_2)+1\Big] = (n+1)\Big[2(l_1+l_2)-n+1\Big] \] Приравнивая результат к \((2l_1+1)(2l_2+1)\), находим: \[ (n+1)\Big[2(l_1+l_2)-n+1\Big] = (2l_1+1)(2l_2+1) \] \[ n^2 - 2(l_1+l_2)n + 4l_1l_2 = 0 \] \[ n_{1,2} = 2l_{1,2} \] Поскольку \(l \ge 0\), то \(l_1 + l_2 -n \ge 0\), откуда видно, что мы должны оставить только меньший из корней: если \(l_1 > l_2\), то \(n = 2l_2\), если же \(l_2 > l_1\), то \(n = 2l_1\). Таким образом, число \(l\) может принимать следующие значения: \[ l = l_1+l_2,\dots,|l_1 - l_2| \] Это называется правилом сложения моментов импульса и справедливо не только для системы двух невзаимодействующих частиц, но и для системы любых двух невзаимодействующих подсистем, а также для моментов импульсов одной и той же частицы (например, при сложении моментов импульса её вращения вокруг собственной оси и вокруг некой внешней оси).
7 Электрон в кулоновском потенциале
Теперь у нас имеется весь необходимый инструментарий для решения задачи о строении атома в рамках квантовой механики. С математической точки зрения, это задача о динамике взаимодействующих друг с другом электронов в кулоновском поле ядра. Для атома с произвольным количеством электронов на орбите эта задача, однако, аналитически не решается. Более того, сложности возникают и с численным решением уже для достаточно простых атомов с числом электронов больше двух–трёх. Однако фундаментальные результаты и общие закономерности можно получить и на примере задачи с одним электроном на орбите. Такая задача решается полностью аналитически.
7.1 Водородоподобные атомы
Атомы, имеющие на орбите только один электрон, называются водородоподобными. Примерами таких атомов могут служить собственно изотопы водорода, а также ионы \(\rm{He}^+\), \(\rm{Li}^{2+}\) и т. д.
Если пренебречь движением тяжёлого ядра, то систему можно считать одночастичной и рассматривать движение только электрона. Оно описывается уравнением Шрёдингера вида \[ i\hbar\frac{\partial \Psi}{\partial t} = \hat H\Psi \] где \(\hat H\) — соответствующий оператор Гамильтона.
Нашей задачей будет поиск стационарных решений вида \(\Psi(\vec r, t) = \psi(\vec r)\exp(i\frac{E}{\hbar} t)\), где \(E\) — полная энергия электрона. Такие решения удовлетворяют стационарному уравнению Шрёдингера вида: \[ \hat H\psi = E\psi \] Для удобства будем работать в сферической системе координат \((r, \vartheta,\varphi)\), в которой потенциальная энергия электрона имеет вид: \[ U(\vec r) \equiv U(r) = - \frac{Ze^2}{r} \] где \(Z\) — зарядовое число ядра.
В сферических координатах удобно представить оператор Гамильтона в следующем виде: \[ \hat H = \hat T + \hat U = \frac{\hat p_r^2}{2m} + \frac{\hat {L^2}}{2mr^2} + U(r) \] где \(\hat p_r\) — оператор радиальной составляющей импульса электрона, имеющий следующий вид: \[ \hat p_r^2 = -\hbar^2\Delta_r = -\hbar^2\left(\frac{\partial^2}{\partial r^2} + \frac{2}{r}\frac{\partial}{\partial r}\right) \] Как мы показали в предыдущих лекциях, оператор \(\hat {L^2}\) действует только на угловые координаты частицы, поэтому он коммутирует с операторами \(\hat p_r\) и \(U(r)\), и следовательно, коммутирует с оператором Гамильтона \(\hat H\). Это означает, что собственные функции оператора Гамильтона совпадают с собственными функциями оператора \(\hat {L^2}\), поэтому справедливо следующее равенство: \[ \hat {L^2}\psi = \hbar^2l(l+1)\psi \] Это упрощает стационарное уравнение Шрёдингера до следующего вида: \[ \frac{\partial^2\psi}{\partial r^2} + \frac{2}{r}\frac{\partial\psi}{\partial r} + \frac{2m}{\hbar^2}\left(E + \frac{Ze^2}{r} - \frac{\hbar^2l(l+1)}{2mr^2}\right)\psi = 0 \] Будем решать его методом, аналогичным тому, который мы использовали для анализа квантового гармонического осциллятора. Введём безразмерные величины \[ \beta^2 = -\frac{2mE}{\hbar^2} \\ \] \[ q = \frac{2mZe^2}{\hbar^2} \] где мы учли, что интересуемся только связанными состояниями, для которых \(E < 0\). Получаем уравнение следующего вида: \[ \frac{\partial^2\psi}{\partial r^2} + \frac{2}{r}\frac{\partial\psi}{\partial r} + \left(\frac{q}{r} - \beta^2 - \frac{l(l+1)}{r^2}\right)\psi = 0 \] Будем искать его решение в виде: \[ \psi = \frac{u(r)}{r}e^{-\beta r}f(\vartheta, \varphi) \] После подстановки получаем: \[ \frac{d^2 u}{d r^2} - 2\beta \frac{du}{d r} + \left(\frac{q}{r} - \frac{l(l+1)}{r^2}\right)u = 0 \] Исследуем поведение этого решения на бесконечности, представив его в виде ряда: \[ u = \sum\limits_{k=\gamma}^\infty a_k r^k \] Подставляем решение в таком виде в уравнение и приравниваем нулю коэффициенты при степенях \(r\). Для степени \(\gamma-2\) получаем: \[ \gamma(\gamma-1) - l(l+1) = 0 \] откуда \(\gamma = l+1\) или \(\gamma = -l\). Второе решение даёт нефизичный результат (функция \(\psi\) обращается в бесконечность в точке \(r=0\)), поэтому оставляем только первое.
Для остальных степеней имеем уравнения вида: \[ \left[k(k+1) - l(l+1)\right]a_{k+1} = (2\beta k - q)a_k,\ k = \gamma+1,\gamma+2,\dots \] Отсюда имеем рекуррентное соотношение между коэффициентами ряда: \[ \frac{a_{k+1}}{a_k} = \frac{2\beta k - q}{k(k+1) - l(l+1)} \] Поведение функции \(u(r)\) при больших \(r\) определяется поведением коэффициентов при больших \(k\). Асимптотически они ведут себя как: \[ \frac{a_{k+1}}{a_k} \approx \frac{2\beta}{k+1} \] Но точно так же ведут себя и коэффициенты разложения в ряд функции \(e^{2\beta r}\). Действительно: \[ e^{2\beta r} = \sum\limits_k c_kr^k = \sum\limits_k \frac{1}{k!}(2\beta r)^k \\ \] \[ \frac{c_{k+1}}{c_k} = \frac{2\beta}{k+1} \] Таким образом, функция \(u(r)\) асимптотически ведёт себя на бесконечности, как функция \(e^{2\beta r}\), следовательно, функция \(\psi\) ведёт себя там же как \(e^{\beta r}\), то есть расходится. Это означает, что такие решения нефизичны.
Мы, однако, рассмотрели только такие решения, для которых коэффициенты \(a_k\) не обращаются в нуль. Если для некоторого \(k=n\) коэффициент \(a_{n+1}\) обратится в нуль, то будут равны нулю и все коэффициенты \(a_k\) для \(k>n+1\). Это означает, что функция \(u(r)\) будет представлять собой полином степени \(n\), и функция \(\psi\) на бесконечности будет вести себя как \(e^{-\beta r}\), то есть будет ограничена.
Условие существования таких решений можно получить, приравняв нулю \(a_{n+1}\) в полученной ранее рекуррентной формуле: \[ 2\beta_n n - q = 0 \\ \] \[ \beta_n = \frac{q}{2n} \] Это накладывает условие на энергию электрона: \[ E_n = -\frac{\hbar^2\beta_n^2}{2m} = - \frac{mZ^2e^4}{2\hbar^2n^2} \] Таким образом, мы нашли условие квантования энергии электрона в водородоподобном атоме. Видно, что выражение для энергии стационарных состояний электрона, полученное нами, совпадает с выражением для энергии электрона в теории атома Бора, однако получено оно из более фундаментальных соображений.
Число \(n\) называется главным квантовым числом.
7.1.1 Вырожденность энергетических уровней атома
Одному и тому же \(n\) в нашем выводе соответствует несколько различных состояний, отличающихся числами \(l\) и \(m\). В этом случае говорят о вырождении энергетического уровня. Число таких состояний называется степенью или кратностью вырождения.
Найдём кратность вырождения для уровня с квантовым числом \(n\). Воспользуемся найденным нами условием \(\gamma = l+1\). Тогда функция \(u_n(r)\) представляет собой сумму: \[ u = \sum\limits_{k=l+1}^n a_k r^k = r^{l+1} \sum\limits_{\alpha=0}^{n-l-1} a_{\alpha+l+1}r^\alpha \] Эта сумма существует для значений \(l=0,1,\dots,n-1\). Для каждого \(l\) число \(m\) может принимать \(2l+1\) значений, поэтому полная кратность вырождения равна: \[ \sum\limits_{l=0}^{n-1} (2l+1) = n^2 \] Необходимо также учесть, что электроны могут иметь внутренние степени свободы. Позднее мы узнаем, что каждый электрон обладает характеристикой, называемой спином, которая может принимать два значения. Таким образом, полная кратность вырождения равна \(2n^2\).
7.1.2 Квантовые числа
Напомним, что числа \(n\), \(l\), \(m\) носят название главного, орбитального и магнитного квантового числа соответственно. Помимо них иногда вводят также радиальное квантовое число \(n_r = n-l-1\), равное числу членов в разложении функции \(u(r)\) по степеням, то есть это число определяет число нулей этой функции.
Отметим также, что исторически состояния с различными \(l\) принято обозначать буквами: \[ l=0 \rightarrow s \\ \] \[ l=1 \rightarrow p \\ \] \[ l=2 \rightarrow d \\ \] \[ l=3 \rightarrow f \\ \] \[ l=4 \rightarrow g \\ \] \[ \cdots \]
7.1.3 Примеры радиальных распределений некоторых состояний
Рассмотрим внешний вид радиальных зависимостей функции \(\psi(r,\vartheta,\varphi)\) для простейших случаев.
7.1.3.1 1s
В состоянии \(1s\) квантовые числа равны \(n=1\), \(l=0\), \(m=0\). Следовательно, \[ u = a_1r \\ \] \[ \psi = a_1e^{-\beta r}f(\vartheta,\varphi) \] Физический смысл, однако, имеет вероятность \(dP = |\psi|^2dV\) обнаружения электрона в объёме \(dV\). В случае исследования радиальной зависимости в качестве объёма \(dV\) выступает тонкий шаровой слой радиусом \(r\) и толщиной \(dr\), его объём: \(dV = 4\pi r^2dr\), следовательно, вероятность равна: \[ dP = 4\pi|\psi|^2r^2dr \] Откуда плотность вероятности: \[ \rho(r) = 4\pi r^2|\psi|^2 \sim r^2e^{-2\beta r} = r^2e^{-qr} \] Эта функция имеет максимум в точке \(r=\frac{2}{q}=\frac{\hbar^2}{me^2}\), что совпадает с выражением для боровского радиуса \(r_B\).
7.1.3.2 2s
В состоянии \(2s\) квантовые числа равны \(n=2\), \(l=0\), \(m=0\). Следовательно, \[ u = a_1r+a_2r^2 \\ \] \[ \frac{a_2}{a_1} = -\frac{q}{4} \\ \] \[ \rho(r) \sim r^2 \left(1-\frac{qr}{4}\right)^2 e^{-qr/2} \] Эта функция имеет нуль в точке \(r=\frac{4}{q}=2r_B\)
7.1.3.3 3s
В состоянии \(3s\) квантовые числа равны \(n=3\), \(l=0\), \(m=0\). Следовательно, \[ u = a_1r+a_2r^2+a_3r^3 \\ \] \[ \frac{a_2}{a_1} = -\frac{q}{3} \\ \] \[ \frac{a_3}{a_2} = -\frac{q}{18} \\ \] \[ \rho(r) \sim r^2 \left(1-\frac{qr}{3} + \frac{(qr)^2}{54}\right)^2 e^{-qr/4} \]
7.1.3.4 2p
Состояние \(1p\) не существует, поскольку \(l\) не может быть больше, чем \(n-1\), а в состоянии \(2p\) квантовые числа имеют значения \(n=2\), \(l=1\) и число \(m\) может принимать три значения \(-1, 0, 1\), что даёт нам три различных состояния. Найдём радиальную плотность вероятности: \[ u = a_2r^2 \\ \] \[ \rho(r)\sim r^4 e^{-qr/2} \] Эта функция имеет один максимум в точке \(r=\frac{8}{q}=4r_B\).
8 Магнитные свойства атомов
В рассмотренной выше задаче мы ограничились учётом только электростатического взаимодействия между ядром и электроном. Однако, вообще говоря, электрон, обладающий моментом импульса, может взаимодействовать и с магнитными полями. Источником таких полей может быть ядро (если оно обладает магнитным моментом), другие электроны, а также сам рассматриваемый электрон (как мы увидим позже, он обладает собственным, внутренним, магнитным моментом). И хотя это взаимодействие в большинстве случаев мало, в отдельных ситуациях учёт его необходим. Кроме того, учёт магнитных свойств электронов требуется для объяснения магнитных свойств веществ. Поэтому в данной главе мы рассмотрим некоторые вопросы квантовой теории атомного магнетизма.
8.1 Исторические замечания
Точное время, когда человечество столкнулось с явлением магнетизма неизвестно. Доподлинно известно, однако, что уже в Древних Китае, Индии и Греции были знакомы с природными магнитами, в частности, с магнетитом или магнитным железняком. На его основе в Древнем Китае, по всей видимости, были изобретены компасы. В Европе первые компасы появляются только в XII–XIII веках н. э.
До XIX века, однако, природа магнетизма оставалась загадкой. Первые шаги в её разгадывании были сделаны Андре Мари Ампером. В 1820 году Ханс Кристиан Эрстед открыл, что протекающий по проводнику ток способен воздействовать на магнитные тела, находящиеся рядом. Ампер же знал, что ток может взаимодействовать с другим током, поэтому предположил, что магнетизм связан с некими молекулярными токами, текущими в веществе. Эта гипотеза противостояла более ранней гипотезе Вильгельма Вебера, согласно которой магнитные вещества состоят из неделимых элементарных магнитиков, являющихся миниатюрными магнитными диполями.
На тот момент, правда, даже не существовало ещё понятие «магнитное поле», появившееся в работах Майкла Фарадея только через 10 лет, а последовательная теория электромагнетизма была создана Джеймсом Максвеллом лишь в 1873 году. Ещё меньше учёные знали об устройстве материи, поэтому более-менее состоятельная элементарная теория природного магнетизма появилась только в 1905 году.
Её автором стал Поль Ланжевен, который построил полуклассическую теорию, основанную на электронной теории Лоренца. Эта теория неявным образом вводила гипотезы о квантовых свойствах атомов, в частности, предполагая наличие стационарных орбит и дипольных моментов у атомов вещества, но работала только для пара- и диамагнетиков, то есть не могла объяснить ферромагнетизм. При этом теория Ланжевена давала в своей области применимости весьма неплохие результаты, и поэтому долгое время пользовалась заметным успехом.
Невозможность построить удовлетворительную теорию магнетизма в рамках чисто классической физики показали независимо Нильс Бор в 1911 году и Хендрикой ван Лёвен (это устоявшаяся транскрипция, хотя правильнее было бы ван Леувен) в районе 1920 года. Теорема Бора — ван Лёвен утверждает:
В состоянии термодинамического равновесия система электрически заряженных частиц (электронов, атомных ядер и т. п.), помещённая в постоянное магнитное поле, не могла бы обладать магнитным моментом, если бы она строго подчинялась законам классической физики.
Наиболее существенным здесь является упоминание термодинамического равновесия. В неравновесной среде возникновение намагниченности не запрещено.
Запрет, вводимый этой теоремой, грубо говоря, связан с тем, что магнитное поле не способно изменить энергию частиц, из которых состоит вещество, и следовательно, не способно сдвинуть точку его термодинамического равновесия.
8.2 Квантовая теория магнитного момента
8.2.1 Классическая связь между магнитным моментом и моментом импульса
Перед тем как построить квантовую теорию магнетизма, рассмотрим классическую связь между движением заряженного тела и его магнитным моментом. Рассмотрим замкнутых виток постоянного тока \(i\), заданный единичным вектором нормали \(\vec n\) к поверхности, натянутой на контур, и величиной площади этой поверхности \(S\). Из курса электродинамики известно, что магнитный момент витка определяется выражением: \[ \vec\mu = \frac{iS}{c}\vec n \] С другой стороны, справедливо соотношение: \[ S \vec n = \frac{1}{2}\oint \left[ \vec r \times \vec{dr} \right] \] Таким образом, имеем: \[ \vec\mu = \frac{1}{2c}\oint i\left[ \vec r \times \vec{dr} \right] \] Этот интеграл можно преобразовать от интегрирования по контуру к интегрированию по зарядам, которые собственно по этому контуру движутся и создают магнитный момент. Пусть элементарный заряд \(dq\) смещается за время \(dt\) на \(\vec{dr}\), тогда создаваемый им ток равен \(i=\frac{dq}{dt}\), а скорость — \(\vec v = \frac{\vec{dr}}{dt}\). В итоге имеем: \[ \vec\mu = \frac{1}{2c}\oint \frac{dq}{dt}\left[ \vec r \times \vec{dr} \right] = \frac{1}{2c}\int\limits_Q \left[ \vec r \times \frac{\vec{dr}}{dt} \right]dq = \frac{1}{2c}\int\limits_Q \left[ \vec r \times \vec v \right]dq \] Интегрирование здесь подразумевается по всему заряду. Отметим, что в таком виде это выражение уже не привязано к какому-либо витку с током и носит значительно более общий характер.
Поскольку мы знаем, что в реальности заряд не является бесконечно делимым, а состоит из элементарных зарядов, то последнее выражение можно переписать в виде: \[ \vec\mu = \frac{1}{2c}\sum\limits_i q_i \left[ \vec{r_i} \times \vec{v_i} \right] \] Рассмотрим движение только одного заряда из этой сумму и перейдём от скоростей к импульсам: \[ \vec\mu_i = \frac{q_i}{2mc}\left[ \vec{r_i} \times \vec{p_i} \right] \] Вспоминая, что момент импульса \(\vec L = \left[ \vec{r} \times \vec{p} \right]\), окончательно получаем: \[ \vec\mu = \frac{q}{2mc}\vec L \] где индексы за ненадобностью опущены. Это связь, устанавливаемая классической физикой между магнитным моментом частицы и её моментом импульса. Соотношение \[ \Gamma = \frac{q}{2mc} \] носит название гиромагнитного отношения. Для электрона имеем: \[ \Gamma = -\frac{e}{2mc} \]
8.2.2 Квантование магнитного момента
В квантовой механике соотношению между динамическими переменными — в нашем случае магнитным моментом и моментом импульса — соответствует соотношение между соответствующими операторами: \[ \hat{\vec\mu} = \Gamma\hat{\vec L} \] Это соотношение сразу говорит нам о том, что правила квантования магнитного момента с точностью до множителя, равного гиромагнитному отношению, совпадают с правилами квантования момента импульса. В частности:
- Величина магнитного момента не зависит от выбора начала координат.
- Величины \(\mu_x\) и \(\mu_y\), а также вообще проекции магнитного момента на две различные оси, неизмеримы одновременно.
- Однако существуют состояния, в которых имеют определённое значение, и следовательно, одновременно измеримы квадрат модуля магнитного момента \(\mu^2\) и одна из его проекций, например, \(\mu_x\).
- Проекция магнитного момента при измерении может принимать следующие значения: \[ \mu_x = \Gamma L_x = \Gamma \hbar m,\ m = 0, \pm 1, \pm 2, \dots \]
- Квадрат модуля магнитного момента при измерении может принимать следующие значения: \[ \mu^2 = \Gamma^2 L^2 = \Gamma^2 \hbar^2 l(l+1),\ l = 0, 1, 2, \dots \]
Для электрона два последних соотношения принимают вид: \[ \mu_x = -\frac{e}{2mc} \hbar m = - \mu_B m \] \[ \mu^2 = \mu_B^2 l(l+1) \] где \(\mu_B = \frac{e\hbar}{2m_e c} = 0,9724\) эрг/Гс — так называемый магнетон Бора.
8.3 Опыт Штерна — Герлаха
Как мы видим, согласно квантовым представлениям проекция и модуль магнитного момента должны квантоваться, то есть принимать при измерении только строго определённый дискретный набор значений. На это было обращено внимание ещё до построения последовательной квантовой теории. Поскольку квантование момента импульса фигурировало уже в теории атома Бора, то из неё следовало и квантование магнитного момента. Первыми об этом, видимо, независимо друг от друга заявили в 1916 году Петер Дебай и Арнольд Зоммерфельд. Эта гипотеза, однако, требовала экспериментальной проверки.
Такой проверкой занялись в Университете Франкфурта Отто Штерн и Вальтер Герлах. Для измерения магнитных моментов атомов они воспользовались тем фактом, что на магнитный момент в сильно неоднородном магнитном поле действует отклоняющая сила, определяемая выражением: \[ \vec F = \left(\vec\mu \nabla\right)\vec H \]
Основной сложностью с точки зрения эксперимента являлось создание достаточно сильно неоднородного магнитного поля. Для этого Штерн и Герлах воспользовались эффекта усиления поля вблизи острия, сделав один из полюсов магнита, создававшего поле, сильно заострённым. Поле при этом оказывалось неоднородным в основном вдоль направления вектора напряжённости.
В этом случае на атом, пролетающий перпендикулярно линиям поля, действует сила: \[ F_z = \mu_x\frac{\partial H_z}{\partial x} + \mu_y\frac{\partial H_z}{\partial y} + \mu_z\frac{\partial H_z}{\partial z} \] где ось \(z\) выбрана направленной вдоль вектора \(\vec H\). При полёте атом совершает прецессию вокруг оси \(z\), причём можно показать, что период этой прецессии \(T = \frac{4\pi\mu c}{eH}\) значительно меньше времени пролёта. Это означает, что влиянием на результат первых двух членов в выражении выше можно пренебречь, поскольку в среднем они дадут нуль. Таким образом, усреднённая сила равна: \[ F_z = \mu_z\frac{\partial H_z}{\partial z} \]
Рассмотрим вопрос, как должен выглядеть результат опыта на экране позади магнита. С классической точки зрения, магнитные моменты атомов распределены случайным образом, и следовательно, величина \(\mu_z\) может принимать произвольное значение из некоторого диапазона. Для атомов, у которых магнитные моменты определяются единственным электроном, этот диапазон составляет \(\left[-\mu_B, \mu_B\right]\). Следовательно, атомы будут испытывать различное отклонение и на экране должен появиться более-менее равномерно засвеченный отрезок.
С точки зрения теории Бора — Зоммерфельда должна наблюдаться иная картина. Согласно этой картине, магнитный момент квантуется, и следовательно, проекция \(\mu_z\) может принимать только дискретный ряд значений \(\mu_B m\), где \(m = 0, \pm 1, \pm 2, \dots\) Для атомов, у которых магнитные моменты определяются единственным электроном, это даёт всего три возможных значения: \(-\mu_B, 0, \mu_B\). Таким образом, на экране должно появиться три (или любое другое — в зависимости от количества электронов, дающих нескомпенсированный вклад в магнитный момент, — нечётное число) точки.
В реальности же, Штерн и Герлах, проводившие опыт с атомами серебра, увидели всего две точки, равноотстоящие от центра. Позднее они провели опыты и с атомами других веществ. Для них картина могла быть более сложной — где-то получалось три, где-то четыре и больше точек. Неизменным оставался лишь сам эффект квантования.
Дополнительную неясность вносили проведённые ещё в 1914–1915 годах эксперименты Эйнштейна и де Гааза, а также Барнета, в которых измерялось гиромагнитное отношение для различных материалов и было показано, что оно зачастую заметно выше классического значения, а для ферромагнетиков и вовсе равно \[ \Gamma = -\frac{e}{mc} \] то есть в два раза выше классического значения.
8.4 Спин
Разрешить эти проблемы удалось благодаря гипотезе, выдвинутой в 1925 году Уленбеком и Гаудсмитом. Дело в том, что к этому времени в связи с увеличением чувствительности спектрометров у многих известных до этого спектральных линий атомов было обнаружено не имевшее объяснения расщепление не две и более линии. Вольфганг Паули в 1924 году предложил объяснить это расщепление наличием у электронов ещё одной степени свободы, не учитывавшейся ранее, однако не стал выдвигать никаких предположений о природе этой степени свободы. Гаудсмит и Уленбек предположили, что эта степень свободы может быть связана с собственным моментом импульса электрона. Этот момент импульса получил название спин.
Интересно, что аналогичное предположение в частных разговорах выдвигал в начале 1925 года и Ральф Крониг, но был раскритикован тем же Паули, указавшим, что если бы электрон обладал собственным моментом импульса, то его величина должна была быть столь большой, что точки электрона, представляемого как сфера с радиусом, равным классическому радиусу электрона, должны были двигаться со скоростью на несколько порядков выше скорости света.
Это возражение, однако, оказалось неверным. Дело в том, что электрон нельзя представлять в виде какого-либо шарика, имеющего конечные размеры. Электрон — существенно квантовый объект, и к нему неприменимы механические представления. При этом он действительно обладает внутренней степенью свободы, проявляющейся как момент импульса.
Спин принято обозначать \(\vec{L_s}\) или \(\vec s\). Именно спин валентного электрона атома серебра вызывал наблюдавшееся Штерном и Герлахом расщепление пучка.
Спин естественным образом появляется в релятивистском обобщении уравнения Шрёдингера — уравнении Дирака, выведенном в 1928 году. При этом показывается, что спин — существенно релятивистский эффект.
Аналогично любому другому моменту импульса спин и его проекции квантуются. При этом вводятся спиновое квантовое число \(s\) и квантовое число \(m_s\) так что: \[ s_z = \hbar m_s \] \[ s^2 = \hbar^2 s(s+1) \] \[ m_s = -s\dots s \] Особенностью спина является то, что спиновое квантовое число может принимать полуцелые значения. Так, для электрона \(s=\frac{1}{2}\), поэтому его проекция может принимать всего два значения: \(m_s=\pm\frac{1}{2}\).
Другой существенной особенностью спина является соотношение между его величиной и связанным с ним магнитным моментом. Дело в том, что электрон обладает собственным магнитным моментом, проекция которого на произвольную ось равна магнетону Бора, то есть: \[ \mu_s = \mu_B = \frac{e\hbar}{2m_e c} \] Таким образом, гиромагнитное отношение для спина равно: \[ \Gamma = \frac{\mu_s}{m_s} = \frac{e}{m_e c} \] То есть оно ровно в два раза выше, чем гиромагнитное отношение для «классического» вращательного движения. Если обозначить «классическое» значение через \(\Gamma_0 = e/2m_e c\), то можно записать: \[ \Gamma = g\Gamma_0 \] где \(g\) называется g-фактором или множителем Ланде, и для свободного электрона он равен \(g=2\).
8.5 Полные механический и магнитный моменты электрона
Поскольку в атоме электрон, с одной стороны, обладает собственными механическим и магнитным моментами, а с другой — совершает орбитальное движение, с которым также связаны механический и магнитный моменты, то полные моменты электрона будут являться суммами спиновых и орбитальных компонент. Условно это можно записать как векторное равенство: \[ \vec J = \vec L + \vec S \] где \(\vec J\) называют полным моментом импульса электрона. Вспоминая правила сложения моментов импульса, находим возможные значения квантового числа \(j\), определяющего величину полного момента импульса: \[ j = |l-s|,\dots,l+s \] Если \(l=0\), то число \(j\) принимает единственное возможное значение: \(j=\frac{1}{2}\). Если \(l>0\), то \(j=l\pm\frac{1}{2}\). Такие уровни образуют дублеты.
Число \(j\) также иногда называют внутренним квантовым числом.
Таким образом, к тройке квантовых чисел \(n\), \(l\), \(m_l\), описывающих состояние электрона в водородоподобном атоме, мы должны добавить ещё одно квантовое число. В его качестве мы можем выбрать, например, \(m_s\), но чаще используют другую четвёрку квантовых чисел: \(n\), \(j\), \(l\), \(m_s\). При этом соответствующий энергетический уровень обозначают следующим образом: \[ n^{2s+1}x_{j} \] где \(x\) — буква, обозначающая число \(l\) (\(s\) для \(l=0\), \(p\) для \(l=1\) и т. д.). Величина (\(2s+1\)) называется мультиплетностью, для уровней энергии водородоподобного атома она всегда равна 2, но для атомов, в которых больше одного электрона, она может быть другой. Мультиплетность обычно показывает степень вырождения энергетического уровня, связанного с наличием у электронов спина. Однако в случае \(l=0\) хотя мультиплетность формально равна 2, но вырождение отсутствует, поскольку \(j=|l-\frac{1}{2}|\) и \(j=l+\frac{1}{2}\) дают одно и то же значение \(j=\frac{1}{2}\).
Поясним сказанное на примере подуровня, имеющего обозначение: \[ 4^{2}d_{\frac{3}{2}} \] На этом подуровне \(n=4\), \(l=2\), \(j=\frac{3}{2}\). Мультиплетность подуровня равна двум, то есть он является частью дублета. На этом подуровне \(j=l-\frac{1}{2}\), поэтому его парой в дублете является подуровень с \(j=l+\frac{1}{2}=\frac{5}{2}\), то есть это подуровень \(4^{2}d_{\frac{5}{2}}\).
Список литературы
Основная
- Д. В. Сивухин. Общий курс физики. Т. V, Ч. 1. Атомная физика. Т. V, Ч. 2. Ядерная физика.
- М. А. Фаддеев, Е. В. Чупрунов. Лекции по атомной физике.
- Л. Б. Окунь Элементарное введение в физику элементарных частиц. М.: Физматлит, 2006.
Дополнительная
- А. Н. Матвеев. Атомная физика.
- А. Н. Матвеев. Оптика.
- А. М. Попов, О. В. Тихонова. Лекции по атомной физике. М.: МГУ, 2007.
- И. В. Савельев. Курс общей физики. Т. 3.
- Э. Вихман. Квантовая физика (Берклеевский курс физики).
- Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике, Т. 8, 9. Квантовая механика.
- Д. Бом. Квантовая теория.
- Б. Х. Ишмухаметов, М. И. Кацнельсон, А. Ф. Поликарпов. Введение в атомную физику. УрФУ, 2017.
- М. Г. Иванов. Как понимать квантовую механику
- Л. Б. Окунь. Физика элементарных частиц. М.: Наука, 1988.
- nuclphys.sinp.msu.ru — Сайт кафедры общей ядерной физики физического факультета МГУ
- В. В. Сыщенко. Физика элементарных частиц для начинающих. М.—Ижевск: НИЦ «Регулярная и хаотическая динамика», 2013.
- Наука. Величайшие теории: выпуск 11: Революция в микромире. Планк. Квантовая теория. М.: Де Агостини, 2015.
Литература из периодических источников
- С. Я. Килин. «Квантовая информация» УФН, 169, № 5, 507-526 (1999)
- М. Б. Менский. «Квантовая механика: новые эксперименты, новые приложения и новые формулировки старых вопросов» УФН, 170, № 6, 631-647 (2000)
- А. И. Голохвастов. «Квантовая механика глазами экспериментатора» УФН, 172, № 7, 843-846, (2002)
- А. В. Белинский. «Квантовая нелокальность и отсутствие априорных значений измеряемых величин в экспериментах с фотонами» УФН, 173, № 8, 905-909 (2003)
- Б. Б. Кадомцев. «Необратимость в квантовой механике» УФН, 173, № 11, 1221-1240 (2003)
- К. А. Валиев. «Квантовые компьютеры и квантовые вычисления» УФН, 175, № 1, 3-39, (2005)